题目内容
求双曲线 5x2-20y2=100 的实轴和虚轴的长，离心率，焦点和顶点的坐标，并画出它的草图．
考点：双曲线的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：将双曲线方程化为标准方程，求得a，b，c，从而可求双曲线的几何性质．
解答：
解：由双曲线5x2-20y2=100化为
-
=1，可得a2=20，b2=5，
∴a=2
，b=
，c=5
∴实轴长2a=4
，虚轴长2b=2
，
顶点坐标：（2
，0）（-2
，0），
焦点（±5，0），
离心率：e=
=
=
，
渐近线：y=±
x，即y=±
x．
草图如图所示．
解：由双曲线5x2-20y2=100化为| x2 |
| 20 |
| y2 |
| 5 |
∴a=2
| 5 |
| 5 |
∴实轴长2a=4
| 5 |
| 5 |
顶点坐标：（2
| 5 |
| 5 |
焦点（±5，0），
离心率：e=
| c |
| a |
| 5 | ||
2
|
| ||
| 2 |
渐近线：y=±
| b |
| a |
| 1 |
| 2 |
草图如图所示．
点评：本题以双曲线方程为载体，考查双曲线的标准方程，考查双曲线的几何性质，属于基础题．
练习册系列答案
相关题目
“?x∈R，x2+x+1＞0“的否定是（ ）
| A、?x0∈R，x02+x0+1＞0 |
| B、?x0∈R，x02+x0+1≤0 |
| C、?x∈R，x2+x+1＞0 |
| D、?x∈R，x2+x+1≤0 |
设全集A={x|x2-2x-15＜0}，B={x|y=lg（x+2）}，则A∩B表示的集合是（ ）
| A、[2，3] |
| B、（-2，5） |
| C、[0，2] |
| D、（2，+∞） |
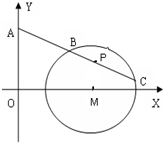如图，过点A（0，a）作直线l，交圆M：（x-2）2+y2=1于点B、C，在BC上取一点P，使P点满足