题目内容
已知向量
=(
sinx，cosx)，
=(cosx，sinx)，f(x)=2
•
-1
（1）求函数f（x）的单调减区间及其图象的对称轴方程；
（2）当x∈[0，π]时，若f（x）=-1，求x的值．
| a |
| 3 |
| b |
| a |
| b |
（1）求函数f（x）的单调减区间及其图象的对称轴方程；
（2）当x∈[0，π]时，若f（x）=-1，求x的值．
考点：平面向量数量积的运算,三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：（1）利用向量的数量积定义表示出函数再利用三角函数的单调减区间及其图象的对称轴方程公式求得．
（2）据已知列出三角方程，注意解三角方程必须先求出角的范围再求出特殊角．
（2）据已知列出三角方程，注意解三角方程必须先求出角的范围再求出特殊角．
解答：
解：（1）f（x）=2
•
-1=2
sinxcosx+2cosxsinx-1=（
+1）sin2x-1．
∴由
+2kπ≤2x≤
+2kπ得
+kπ≤x≤
+kπ，k∈Z．
∴函数f（x）的单调减区间为[
+kπ，
+kπ]，k∈Z．
由2x=
+kπ得，x=
+
，k∈Z．
∴函数f（x）的对称轴方程x=
+
，k∈Z．
（2）由f（x）=-1，得（
+1）sin2x-1=-1．
∴sin2x=0
∵x∈[0，π]，
∴2x=0或2x=π，即x=0或x=
．
| a |
| b |
| 3 |
| 3 |
∴由
| π |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴函数f（x）的单调减区间为[
| π |
| 4 |
| 3π |
| 4 |
由2x=
| π |
| 2 |
| π |
| 4 |
| kπ |
| 2 |
∴函数f（x）的对称轴方程x=
| π |
| 4 |
| kπ |
| 2 |
（2）由f（x）=-1，得（
| 3 |
∴sin2x=0
∵x∈[0，π]，
∴2x=0或2x=π，即x=0或x=
| π |
| 2 |
点评：本题考查向量的数量积公式及三角函数的周期公式，解三角方程时注意一定要求出角的范围．
练习册系列答案
相关题目
已知函数f（x）=函数y=(
)x-
的图象可能是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、 |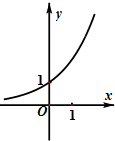
B、 |
C、 |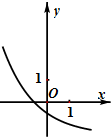
D、 |
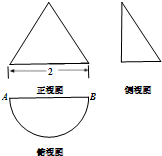一个几何体的三视图如图所示，其中正视图是等边三角形，俯视图是半圆．现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点，则蚂蚁所经过路程的最小值为
如图，一个广告气球被一束入射角为30°的平行光线照射，其投影是一个最长的弦长为5米的椭圆，则制作这个广告气球至少需要的面料是