题目内容
(1)设x>-1,试比较ln(1+x)与x的大小;
(2)是否存在常数a∈N,使得a<
(1+
)k<a+1对任意大于1的自然数n都成立?若存在,试求出a的值并证明你的结论;若不存在,请说明理由.
(2)是否存在常数a∈N,使得a<
| 1 |
| n |
| n |
 |
| k=1 |
| 1 |
| k |
考点:二项式定理的应用,对数值大小的比较,归纳推理
专题:计算题,导数的综合应用,二项式定理
分析:(1)设f(x)=x-ln(x+1),求出导数,求得单调区间,得到最小值,进而比较大小;
(2)取m=1,2,3,4进行验算,得到猜测:①2<(1+
)m<3,m=2,3,4,5,…,②存在a=2,使得a<
(1+
)k<a+1恒成立.运用(1)的结论可证①,运用二项式定理,即可证明②.
(2)取m=1,2,3,4进行验算,得到猜测:①2<(1+
| 1 |
| m |
| 1 |
| n |
| n |
 |
| k=1 |
| 1 |
| k |
解答:
解:(1)设f(x)=x-ln(x+1),则f′(x)=1-
=
,
当-1<x<0时,f′(x)<0,f(x)单调递减;
当x>0时,f′(x)>0,f(x)单调递增;
故函数f(x)有最小值f(0)=0,则ln(x+1)≤x恒成立;
(2)取m=1,2,3,4进行验算:
(1+
)1=2,
(1+
)2=
=2.25,
(1+
)3=
≈2.37,
(1+
)4=
≈2.44,
猜测:①2<(1+
)m<3,m=2,3,4,5,…,
②存在a=2,使得a<
(1+
)k<a+1恒成立.
证明:由(1)知:当0<x≤1时,ln(x+1)<x,
设x=
,k=1,2,3,4,…,
则ln(1+
)<
,所以kln(1+
)<1,ln(1+
)k<1,(1+
)k<e<3,
当k≥2时,再由二项式定理得:
(1+
)k=
+…
>
=2,
即2<(1+
)k<3对任意大于1的自然数k恒成立,
从而有2n<
(1+
)k<3n成立,即a<
(1+
)k<a+1,
所以存在a=2,使得得a<
(1+
)k<a+1恒成立.
| 1 |
| 1+x |
| x |
| x+1 |
当-1<x<0时,f′(x)<0,f(x)单调递减;
当x>0时,f′(x)>0,f(x)单调递增;
故函数f(x)有最小值f(0)=0,则ln(x+1)≤x恒成立;
(2)取m=1,2,3,4进行验算:
(1+
| 1 |
| 1 |
(1+
| 1 |
| 2 |
| 9 |
| 4 |
(1+
| 1 |
| 3 |
| 64 |
| 27 |
(1+
| 1 |
| 4 |
| 625 |
| 256 |
猜测:①2<(1+
| 1 |
| m |
②存在a=2,使得a<
| 1 |
| n |
| n |
 |
| k=1 |
| 1 |
| k |
证明:由(1)知:当0<x≤1时,ln(x+1)<x,
设x=
| 1 |
| k |
则ln(1+
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
当k≥2时,再由二项式定理得:
(1+
| 1 |
| k |
| C | 0 k |
| +C | 1 k |
| 1 |
| k |
| +C | 2 k |
| 1 |
| k2 |
| +C | k k |
| 1 |
| kk |
| C | 0 k |
| +C | 1 k |
| 1 |
| k |
即2<(1+
| 1 |
| k |
从而有2n<
| n |
 |
| k=1 |
| 1 |
| k |
| 1 |
| n |
| n |
 |
| k=1 |
| 1 |
| k |
所以存在a=2,使得得a<
| 1 |
| n |
| n |
 |
| k=1 |
| 1 |
| k |
点评:本题考查构造函数,运用导数求单调区间、最值,进而比较大小,考查二项式定理的运用,考查归纳、猜想、证明的思想方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
点A、B、C、D在同一个球的球面上,AB=BC=AC=
,若四面体ABCD体积的最大值为
,则这个球的表面积为( )
| 3 |
| 3 |
A、
| ||
| B、8π | ||
C、
| ||
D、
|
已知命题p:?x∈R,x-2>0,命题q:?x∈R,
>x,则下列说法中正确的是( )
| x |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∨(¬q)是假命题 |
| D、命题p∧(¬q)是真命题 |
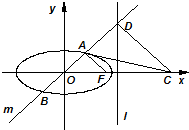 已知椭圆Γ:
已知椭圆Γ: