题目内容
 已知函数f(x)=
已知函数f(x)=
| ||
| 2 |
| 3 |
| 2 |
(Ⅰ)求f(x)的解析式;
(Ⅱ)将f(x)的图象沿x轴向右平移
| 2 |
| 3 |
P、Q分别为函数g(x)图象的最高点和最低点(如图),求∠OQP的大小.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)利用三角恒等变换化简函数的解析式为 f(x)=
sin(ωx+
),根据函数的周期为4=
,求得ω 的值,可得f(x)的解析式.
(2)由条件根据y=Asin(ωx+φ)的图象变换规律,可得函数g(x)=
sin
x,求出P、Q的坐标,利用余弦定理求得cosθ 的值,可得θ的值.
| 3 |
| π |
| 3 |
| 2π |
| ω |
(2)由条件根据y=Asin(ωx+φ)的图象变换规律,可得函数g(x)=
| 3 |
| π |
| 2 |
解答:
解:(1)f(x)=
sinωx+
cosωx(ω>0)=
(
sinωx+
cosωx)=
sin(ωx+
),
由于函数的周期为4=
,得ω=
,
故f(x)=
sin(
x+
).
(2)将f(x)的图象沿x轴向右平移
个单位得到函数g(x)=
sin
x.
因为P、Q分别为该图象的最高点和最低点,
∴P(1,
)、Q (3,-
).
所以OP=2,PQ=4,OQ=
,cosθ=
=
,
∴θ=
.
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
由于函数的周期为4=
| 2π |
| ω |
| π |
| 2 |
故f(x)=
| 3 |
| π |
| 2 |
| π |
| 3 |
(2)将f(x)的图象沿x轴向右平移
| 2 |
| 3 |
| 3 |
| π |
| 2 |
因为P、Q分别为该图象的最高点和最低点,
∴P(1,
| 3 |
| 3 |
所以OP=2,PQ=4,OQ=
| 12 |
| OQ2+PQ2-OP2 |
| 2OQ•QP |
| ||
| 2 |
∴θ=
| π |
| 6 |
点评:本题考查了三角函数和角公式的变换和三角函数图象周期、对称、平移等基本性质,考查运用有关勾股定理、余弦定理求解三角形的能力,属于中档题.

练习册系列答案
相关题目
与函数y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=(
| ||
| C、y=logaax(a>o,a≠1) | ||
D、y=
|
以y=±x为渐近线且经过点(2,0)的双曲线方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
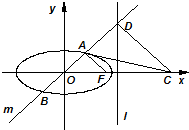 已知椭圆Γ:
已知椭圆Γ: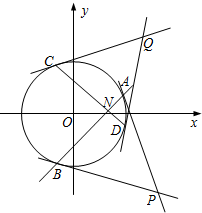 已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.
已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.