题目内容
已知y=-x2+ax-
+
,x∈[-1,1]的最大值为2,求a的值.
| a |
| 4 |
| 1 |
| 2 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:根据对称轴讨论分析最大值,再利用求解方程即可,注意判断是否符合题意.
解答:
解:∵y=-x2+ax-
+
,x∈[-1,1],
∴对称轴x=
,
当
≤-1时,即a≤-2,最大值为f(-1)=-
-
=2,解得:a=-2符合题意,
当
≥1时,即a≥2,最大值为f(1)=
-
=2,解得:a=
符合题意,
当-1<
<1时,-2<a<2,最大值为f(
)=
-
+
=2,解得:a=3或a=-2不符合题意,
综上:a=-2或a=
.
| a |
| 4 |
| 1 |
| 2 |
∴对称轴x=
| a |
| 2 |
当
| a |
| 2 |
| 5a |
| 4 |
| 1 |
| 2 |
当
| a |
| 2 |
| 3a |
| 4 |
| 1 |
| 2 |
| 10 |
| 3 |
当-1<
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 4 |
| 1 |
| 2 |
综上:a=-2或a=
| 10 |
| 3 |
点评:本题考查了二次函数在闭区间上的最值的求解,及应用,属于中档题.

练习册系列答案
相关题目
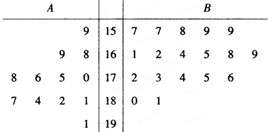 某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售. 已知椭圆Γ:
已知椭圆Γ: