题目内容
在长方体ABCD-A1B1C1D1中,AA1=AD=2,E为CD中点.
(1)求证:B1E⊥AD1;
(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长.若不存在,说明理由.
(1)求证:B1E⊥AD1;
(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长.若不存在,说明理由.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)连接A1D,B1C,证明AD1⊥平面A1B1CD,即可证得结论;
(2)取B1A中点F,连结PF、EF,利用三角形的中位线的性质,可得线线平行,从而可得线面平行.
(2)取B1A中点F,连结PF、EF,利用三角形的中位线的性质,可得线线平行,从而可得线面平行.
解答:
(1)证明:在长方体中,B1A1⊥平面ADD1A1,
∴B1A1⊥AD1
在矩形ADD1A1中,∵AD=AA1=2
∴矩形ADD1A1为正方形
∴A1D⊥AD1
又B1A1∥CD,∴AD1⊥平面CDA1B1
∵E为CD中点
∴B1E⊆平面CDA1B1
∴AD1⊥B1E
(2)解:存在AA1中点P,AP=1时得DP∥平面B1AE
取B1A中点F,连结PF、EF
在△AA1B1中,PF平行且等于
A1B1
在长方体ABCD-A1B1C1D1中,A1B1平行且等于CD,∵E为CD中点,
∴PF平行且等于DE
∴四边形PFED为平行四边形
∴DP∥EF
又EF⊆平面B1AE,DP?平面B1AE,
∴DP∥平面B1AE
∴B1A1⊥AD1
在矩形ADD1A1中,∵AD=AA1=2
∴矩形ADD1A1为正方形
∴A1D⊥AD1
又B1A1∥CD,∴AD1⊥平面CDA1B1
∵E为CD中点
∴B1E⊆平面CDA1B1
∴AD1⊥B1E
(2)解:存在AA1中点P,AP=1时得DP∥平面B1AE
取B1A中点F,连结PF、EF
在△AA1B1中,PF平行且等于
| 1 |
| 2 |
在长方体ABCD-A1B1C1D1中,A1B1平行且等于CD,∵E为CD中点,
∴PF平行且等于DE
∴四边形PFED为平行四边形
∴DP∥EF
又EF⊆平面B1AE,DP?平面B1AE,
∴DP∥平面B1AE
点评:本题考查线面垂直,线面平行,考查学生分析解决问题的能力,掌握线面垂直,线面平行的判定方法是关键.

练习册系列答案
相关题目
点A、B、C、D在同一个球的球面上,AB=BC=AC=
,若四面体ABCD体积的最大值为
,则这个球的表面积为( )
| 3 |
| 3 |
A、
| ||
| B、8π | ||
C、
| ||
D、
|
若A与B是互斥事件,其发生的概率分别为p1,p2,则A∪B发生的概率为( )
| A、p1+p2 |
| B、p1•p2 |
| C、1-p1•p2 |
| D、0 |
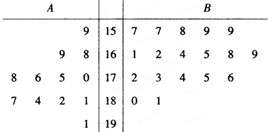 某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.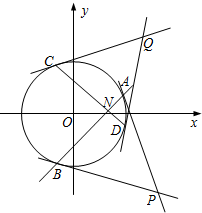 已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.
已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.