题目内容
求f（x）=
sinx+cosx对称轴方程．
| 3 |
考点：两角和与差的正弦函数,正弦函数的对称性
专题：计算题,三角函数的图像与性质
分析：化简函数f（x）的解析式为f（x）=2sin（x+
），令x+
=kπ+
，k∈Z，可得 x=kπ+
，k∈Z就是函数的对称轴，由此得出结论．
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
解答：
解：∵f（x）=
sinx+cosx=2sin（x+
）
∴令x+
=kπ+
，k∈Z，可解得：x=kπ+
，k∈Z，
故f（x）=
sinx+cosx对称轴方程为x=kπ+
，k∈Z．
| 3 |
| π |
| 6 |
∴令x+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
故f（x）=
| 3 |
| π |
| 3 |
点评：本题主要考查三角函数的恒等变换，正弦函数的对称性，化简函数f（x）的解析式是解题的关键，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
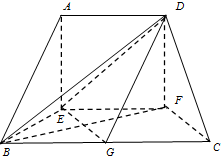已知在如图的多面体中，AE⊥底面BEFC，AD∥EF∥BC，CF=BE=AD=EF=