题目内容
不等式|x-2|≤m的解集为{x|-4≤x≤8},又已知a,b,c∈R,且a+2b+3c=m,求a2+4b2+9c2的最小值.
考点:二维形式的柯西不等式,绝对值不等式的解法
专题:选作题,不等式
分析:根据不等式|x-2|≤m的解集为{x|-4≤x≤8},求出m,利用柯西不等式,得(a+2b+3c)2=(1×a+1×2b+1×3c)2≤(12+12+12)(a2+4b2+9c2)=3(a2+4b2+9c2),化简得a2+4b2+9c2≥12,由此可得a2+4b2+9c2的最小值为12.
解答:
解:不等式|x-2|≤m 的解集为{x|2-m≤x≤2+m},
又不等式|x-2|≤m的解集为{x|-4≤x≤8},所以m=6,
可知a+2b+3c=6,根据柯西不等式,得(a+2b+3c)2=(1×a+1×2b+1×3c)2≤(12+12+12)[a2+(2b)2+(3c)2]
化简得62≤3(a2+4b2+9c2),即36≤3(a2+4b2+9c2)
∴a2+4b2+9c2≥12,
当且仅当a:2b:3c=1:1:1时,即a=2,b=1,c=
时等号成立
由此可得:当且仅当a=2,b=1,c=
时,a2+4b2+9c2的最小值为12
又不等式|x-2|≤m的解集为{x|-4≤x≤8},所以m=6,
可知a+2b+3c=6,根据柯西不等式,得(a+2b+3c)2=(1×a+1×2b+1×3c)2≤(12+12+12)[a2+(2b)2+(3c)2]
化简得62≤3(a2+4b2+9c2),即36≤3(a2+4b2+9c2)
∴a2+4b2+9c2≥12,
当且仅当a:2b:3c=1:1:1时,即a=2,b=1,c=
| 2 |
| 3 |
由此可得:当且仅当a=2,b=1,c=
| 2 |
| 3 |
点评:本题给出等式a+2b+3c=m,求式子a2+4b2+9c2的最小值.着重考查了运用柯西不等式求最值与柯西不等式的等号成立的条件等知识,属于中档题.

练习册系列答案
相关题目
设函数f(x)满足f(x)=1+f(2)•log2x2,则f(4)=( )
| A、-3 | B、-2 | C、0 | D、1 |
下列方程的曲线不关于x轴对称的是( )
| A、x2-x+y2=1 |
| B、x2y+xy2=1 |
| C、2x2-y2=1 |
| D、x+y2=-1 |
若命题P(n)对n=3成立,且由P(k)成立可以推证P(k+2)也成立,则一定有( )
| A、P(n)对所有正整数都成立 |
| B、P(n)对所有正偶数都成立 |
| C、P(n)对所有正奇数都成立 |
| D、P(n)对所有大于等于3的正奇数都成立 |
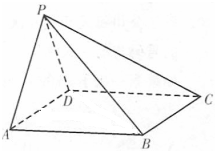 四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.
四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.