题目内容
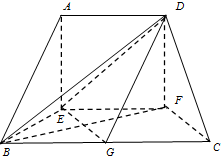 已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF=
已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF=| 1 |
| 2 |
(1)求证:AB∥平面DEG;
(2)求证:EG⊥平面BDF;
(3)求此多面体ABCDEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)根据线面平行的判定定理即可证明AB∥平面DEG;
(2)根据线面垂直的判定定理即可证明EG⊥平面BDF;
(3)根据多面体的体积公式利用割补法即可求此多面体ABCDEF的体积.
(2)根据线面垂直的判定定理即可证明EG⊥平面BDF;
(3)根据多面体的体积公式利用割补法即可求此多面体ABCDEF的体积.
解答:
证明:(1)∵AD∥EF∥BC,
∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴AD∥BG,且AD=BG,
∴四边形ADGB是平行四边形,
∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,
∴AB∥平面DEG.
(2)连结GF,四边形ADFE是矩形,
∵DF∥AE,AE⊥底面BEFC,
∴DF⊥平面BCFE,EG?平面BCFE,
∴DF⊥EG,
∵EF∥BG,EF=BG,EF=BE,
∴四边形BGFE为菱形,∴BF⊥EG,
又BF∩DF=F,BF?平面BFD,DF?平面BFD,
∴EG⊥平面BDF;
(3)VABCDEF=VB-AEFD+VD-BCF,作BH⊥EF于H,
∵平面AEFD⊥平面BEFC,
∴BH⊥平面AEFD,EG∥CF,
∴CF⊥平面BDF,
BH=
,VB-AEFD=
×
×2×2=
,
VD-BCF=VC-BFD=
×2×
×2×2
=
,
∴VABCDEF=
.
∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴AD∥BG,且AD=BG,
∴四边形ADGB是平行四边形,

∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,
∴AB∥平面DEG.
(2)连结GF,四边形ADFE是矩形,
∵DF∥AE,AE⊥底面BEFC,
∴DF⊥平面BCFE,EG?平面BCFE,
∴DF⊥EG,
∵EF∥BG,EF=BG,EF=BE,
∴四边形BGFE为菱形,∴BF⊥EG,
又BF∩DF=F,BF?平面BFD,DF?平面BFD,
∴EG⊥平面BDF;
(3)VABCDEF=VB-AEFD+VD-BCF,作BH⊥EF于H,
∵平面AEFD⊥平面BEFC,
∴BH⊥平面AEFD,EG∥CF,
∴CF⊥平面BDF,
BH=
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
VD-BCF=VC-BFD=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
4
| ||
| 3 |
∴VABCDEF=
| 8 |
| 3 |
| 3 |
点评:本题主要考查空间直线和平面平行和垂直的判定,以及空间多面体的体积的计算,要求熟练掌握相应的判定定理.

练习册系列答案
相关题目
若命题P(n)对n=3成立,且由P(k)成立可以推证P(k+2)也成立,则一定有( )
| A、P(n)对所有正整数都成立 |
| B、P(n)对所有正偶数都成立 |
| C、P(n)对所有正奇数都成立 |
| D、P(n)对所有大于等于3的正奇数都成立 |