题目内容
已知斜率为1的直线l过点(0,
),抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上,求抛物线C的方程.
| 5 |
| 4 |
考点:抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求得直线l的方程,进而可得到原点垂直于l的直线方程,然后联立两方程求得其交点坐标,得到p的值,从而可确定抛物线的方程.
解答:
解:由题意可得直线l:y=x+
①
过原点垂直于l的直线方程为y=-x②
解①②得x=-
.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上,
∴-
=-
×2,
∴p=
,
∴抛物线C的方程为y2=5x.
| 5 |
| 4 |
过原点垂直于l的直线方程为y=-x②
解①②得x=-
| 5 |
| 8 |
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上,
∴-
| p |
| 2 |
| 5 |
| 8 |
∴p=
| 5 |
| 2 |
∴抛物线C的方程为y2=5x.
点评:本题主要考查直线与抛物线的综合题,考查抛物线方程,考查学生的计算能力,比较基础.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知M (0,-2),N (0,4),则以MN为斜边的直角三角形直角顶点P的轨迹方程是( )
| A、x2+y2=4,(y≠±2) |
| B、x2+y2=9 |
| C、x2+(y-1)2=9,(y≠-2且y≠4) |
| D、x2+(y-1)2=9 |
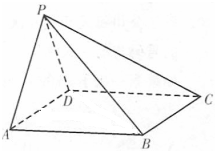 四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.
四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.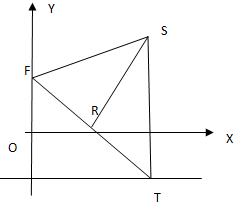 在平面直角坐标系中,O为坐标原点,点 F,T,R,S满足
在平面直角坐标系中,O为坐标原点,点 F,T,R,S满足