题目内容
函数f(x)=cosx+2sinx在区间[0,
]上的最小值为 .
| π |
| 2 |
考点:三角函数的最值
专题:三角函数的图像与性质
分析:把函数化简得:f(x)=cosx+2sinx=
sin(x+θ.),cosθ=
,sinθ=
,可判断θ∈(0,
),再根据函数单调性求出最小值.
| 5 |
| 2 | ||
|
| 1 | ||
|
| π |
| 4 |
解答:
解:∵函数f(x)=cosx+2sinx=
sin(x+θ.),cosθ=
,sinθ=
,
∴可判断θ∈(0,
),
∵θ≤x+θ≤
+θ<
,
∴根据单调性可知
当x+θ=θ时,f(x)min=
sinθ=1,
故答案为:1.
| 5 |
| 2 | ||
|
| 1 | ||
|
∴可判断θ∈(0,
| π |
| 4 |
∵θ≤x+θ≤
| π |
| 2 |
| 3π |
| 4 |
∴根据单调性可知
当x+θ=θ时,f(x)min=
| 5 |
故答案为:1.
点评:本题考查了三角函数的性质,利用单调性求最值,求最大值容易一些,但是求最小值时要根据系数判断哪个地方取到,比较基础.

练习册系列答案
相关题目
已知实数x,y满足约束条件
则z=x+3y的最大值等于( )
|
| A、9 | B、0 | C、27 | D、36 |
在△ABC中,若b=2,A=120°,三角形的面积S=
,则三角形外接圆的半径为( )
| 3 |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
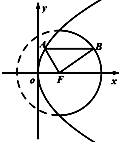 已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是
已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是