题目内容
10.已知函数f(x)=|x-1|+|x+a|(Ⅰ)当a=3时,解关于x的不等式|x-1|+|x+a|>6
(Ⅱ)若函数g(x)=f(x)-|3+a|存在零点,求实数a的取值范围.
分析 (Ⅰ)当a=-1时,不等式|x-1|+|x+3|>6等价变形,可得结论;
(Ⅱ)利用|x-1|+|x+a|≥|a+1|,即可求实数a的取值范围.
解答 解:(Ⅰ)当a=3时,不等式|x-1|+|x+3|>6可化为
$\left\{\begin{array}{l}{x≤-3}\\{1-x-x-3>6}\end{array}\right.$或$\left\{\begin{array}{l}{-3<x<1}\\{1-x+x+3>6}\end{array}\right.$或$\left\{\begin{array}{l}{x>1}\\{x-1+x+3>6}\end{array}\right.$,…(3分)
解得x<-4或x>2,
∴不等式f(x)>5的解集为{x|x<-4或x>2}.…(5分)
(Ⅱ)若函数g(x)=f(x)-|3+a|存在零点,则
∵|x-1|+|x+a|≥|a+1|,
∴|3+a|≥|a+1|,解得a≥-2.
点评 本题考查绝对值不等式,考查学生的计算能力,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.α是一个平面,m,n是两条直线,A是一个点,若m?α,n?α,且A∈m,A∈α,则m,n的位置关系不可能是( )
| A. | 垂直 | B. | 相交 | C. | 异面 | D. | 平行 |
5.已知a,b∈R,定义运算“?”:a?b=$\left\{\begin{array}{l}{aa-b≤1}\\{ba-b>1}\end{array}\right.$,函数f(x)=(x2-2)?(x-1),x∈R,若方程f(x)-a=0只有两个不同实数根,则实数a的取值范围是( )
| A. | [-2,-1]∪(1,2) | B. | (-2,-1]∪(1,2] | C. | [-2,-1]∪[1,2] | D. | (-2,-1]∪(1,2) |
15.平面直角坐标系中,在由x轴、$x=\frac{π}{3}$、x=$\frac{5π}{3}$和y=2所围成的矩形中任取一点,满足不等关系y≤1-sin3x的概率是( )
| A. | $\frac{4π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19.“函数f(x)=a+lnx(x≥e)存在零点”是“a<-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不用必要条件 |
4.已知双曲线${x^2}-\frac{y^2}{2}=1$的焦点为F1,F2,则焦距|F1F2|=( )
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 6 |
 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.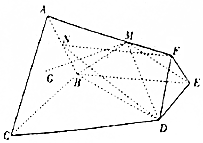 如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.
如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.