题目内容
2．已知曲线f（x）=ax3+bx2在x=1处的切线为y=3x-1，求：（1）求f（x）的解析式；
（2）求过原点的f（x）的切线方程．
分析 （1）求出f（x）的导数，可得在x=1处切线的斜率，由已知切线的方程可得a，b的方程组，解方程可得a，b，进而得到f（x）的解析式；
（2）设出切点（m，-m3+3m2），求得f（x）的导数，可得切线的斜率，由点斜式方程可得切线的方程，代入原点，解方程可得m，进而得到切线的方程．
解答 解：（1）f（x）=ax3+bx2的导数为f′（x）=3ax2+2bx，
由在x=1处的切线为y=3x-1，
可得f（1）=a+b=2，f′（1）=3a+2b=3，
解方程可得a=-1，b=3，
则f（x）=-x3+3x2；
（2）设切点为（m，-m3+3m2），
f（x）=-x3+3x2的导数为f′（x）=-3x2+6x，
可得过原点的f（x）的切线斜率为-3m2+6m，
切线的方程为y-（-m3+3m2）=（-3m2+6m）（x-m），
由于切线经过（0，0），可得
0-（-m3+3m2）=（-3m2+6m）（0-m），
化为3m2=2m3，解得m=0或$\frac{3}{2}$，
即有切线的方程为y-0=0（x-0）或y-0=$\frac{9}{4}$（x-0），
即为y=0或y=$\frac{9}{4}$x．
即y=0或9x-4y=0．
点评 本题考查导数的运用：求切线的方程，考查导数的几何意义，注意区分在某点处和过某点的切线，正确求导和运用点斜式方程是解题的关键，属于中档题和易错题．
练习册系列答案
相关题目
12．已知曲线C：$\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$（t为参数），A（-1，0），B（1，0），若曲线C上存在点P满足$\overrightarrow{AP}$•$\overrightarrow{BP}$=0，则实数a的取值范围为（ ）
| A． | $[{-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}}]$ | B． | [-1，1] | C． | $[{-\sqrt{2}，\sqrt{2}}]$ | D． | [-2，2] |
13．在区间[0，1]上随机选取两个数x和y，则y＞3x的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{12}$ |
17．某四棱锥的三视图如图所示，则该四棱锥的底面的面积是（ ）
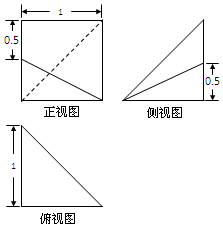
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
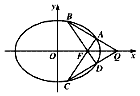如图，过椭圆M：$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A，C两点．