题目内容
1. 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.(Ⅰ)证明:BD⊥平面SAD;
(Ⅱ)求点C到平面SAB的距离.
分析 (Ⅰ)证明:AD⊥BD,SA⊥BD,即可证明BD⊥平面SAD;
(Ⅱ)利用等体积方法,求点C到平面SAB的距离.
解答 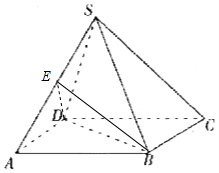 (Ⅰ)证明:△ADB中,由余弦定理可得BD=2,∴BD2+AD2=AB2,∴AD⊥BD.
(Ⅰ)证明:△ADB中,由余弦定理可得BD=2,∴BD2+AD2=AB2,∴AD⊥BD.
取SD的中点E,连接DE,BE,则DE⊥SA,BE⊥SA,
∵DE∩BE=E,∴SA⊥平面BDE,
∴SA⊥BD,
∵SA∩AD=A,
∴BD⊥平面SAD;
(Ⅱ)解:点C到平面SAB的距离=点D到平面SAB的距离h.
△SAD中,SAD=30°,AD=SD=2$\sqrt{3}$,∴S△SAD=$\frac{1}{2}×2\sqrt{3}×2\sqrt{3}×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
△SAB中,BA=BS=4,SA=6,∴S△SAB=$\frac{1}{2}×6×\sqrt{16-9}$=3$\sqrt{7}$,
由等体积可得$\frac{1}{3}×3\sqrt{3}×2=\frac{1}{3}×3\sqrt{7}h$,∴h=$\frac{2\sqrt{21}}{7}$.
点评 本题考查线面垂直的殴打,考查点面距离,考查体积的计算,属于中档题.

练习册系列答案
相关题目
11.已知函数f(x)是定义在R上的可导函数,其导函数为f′(x),则命题P:“?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017”是命题Q:“?x∈R,|f′(x)|<2017”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知曲线C:$\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),A(-1,0),B(1,0),若曲线C上存在点P满足$\overrightarrow{AP}$•$\overrightarrow{BP}$=0,则实数a的取值范围为( )
| A. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | [-2,2] |
9.已知过抛物线y2=2px(p>0)的焦点F的直线与抛物线交于A,B两点,且$\overrightarrow{AF}$=3$\overrightarrow{FB}$,抛物线的准线l与x轴交于点C,AA1⊥l于点A1,若四边形AA1CF的面积为12$\sqrt{3}$,则准线l的方程为( )
| A. | x=-$\sqrt{2}$ | B. | x=-2$\sqrt{2}$ | C. | x=-2 | D. | x=-1 |
16.已知抛物线y2=2px(p>0)过点A($\frac{1}{2}$,$\sqrt{2}$),其准线与x轴交于点B,直线AB与抛物线的另一个交点为M,若$\overrightarrow{MB}$=λ$\overrightarrow{AB}$,则实数λ为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
13.在区间[0,1]上随机选取两个数x和y,则y>3x的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
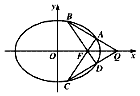 如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.
如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.