题目内容
已知| OA |
| a |
| OB |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的数量积性质、基本不等式的性质、三角形的面积计算公式即可得出．
解答：
解：∵
•
=丨
-
丨=2，∴
2+
2-2
•
=4，
∴
2+
2=8≥2|
||
|，∴|
||
|≤4，当且仅当|
|=|
|=2时取等号，
此时|
||
|cosθ=2，化为cosθ=
，θ=
．
∵S△=
|
| |
|sinθ，
∴4
=|
|2|
|2sin2θ=|
|2|
|2-(
•
)2=|
|2|
|2-4≤42-4=12，
∴S△≤
．此时cosθ=
．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
此时|
| a |
| b |
| 1 |
| 2 |
| π |
| 3 |
∵S△=
| 1 |
| 2 |
| a |
| b |
∴4
| S | 2 △ |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴S△≤
| 3 |
| π |
| 3 |
点评：本题考查了向量的数量积性质、基本不等式的性质、三角形的面积计算公式，属于中档题．
练习册系列答案
相关题目
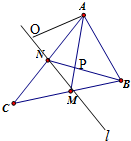在△ABC中，已知AB=2，AC=6，∠BAC=60°，中线AM、BN交于点P，设
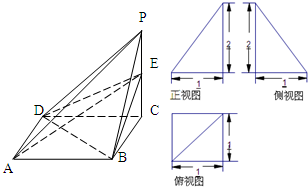已知四棱锥P-ABCD的三视图和直观图如图所示，其中正视图、侧视图是直角三角形，俯视图是有一条对角线的正方形．E是侧棱PC上的动点．