题目内容
在正项等比数列{an}中,3a1,
a3,2a2成等差数列,则
= .
| 1 |
| 2 |
| a2013+a2014 |
| a2011+a2012 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:设公比为q,由a1q2=3a1+2a1q,求得q的值,再根据等比数列的性质求得要求的式子为q2,从而得出结论.
解答:
解:正项等比数列{an}中,设公比为q,由3a1,
a3,2a2成等差数列,
可得a1q2=3a1+2a1q,求得q=3,或q=-1(舍去).
∴
=
=q2=9,
故答案为:9.
| 1 |
| 2 |
可得a1q2=3a1+2a1q,求得q=3,或q=-1(舍去).
∴
| a2013+a2014 |
| a2011+a2012 |
| a2011•q2+a2012•q2 |
| a2011+a2012 |
故答案为:9.
点评:本题主要考查等比数列的定义和性质,等差中项的定义,求出公比,是解题的关键,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 已知
已知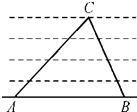 如图,为了测定河的宽度,在一岸边选定两点A,B和对岸标记物C,测得∠CAB=30°,∠CBA=45°,AB=120m,则河的宽度为
如图,为了测定河的宽度,在一岸边选定两点A,B和对岸标记物C,测得∠CAB=30°,∠CBA=45°,AB=120m,则河的宽度为