题目内容
已知函数f（x）=cos2x-
sin2x，x∈R．
（1）求函数f（x）的单调递减区间；
（2）设θ∈（
，
），且f（θ）=-
，求cos2θ．
| 3 |
（1）求函数f（x）的单调递减区间；
（2）设θ∈（
| π |
| 3 |
| 7π |
| 12 |
| 4 |
| 3 |
考点：两角和与差的正弦函数,二倍角的余弦
专题：三角函数的求值
分析：（1）由和差角公式化简可得f（x）=2cos（2x+
），整体法令2kπ≤2x+
≤2kπ+π，解不等式可得；（2）可得cos（2θ+
）=-
，进而可得sin（2θ+
），而cos2θ=cos[（2θ+
）-
]=
cos（2θ+
）+
sin（2θ+
），代入计算可得．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
解答：
解：（1）∵f（x）=cos2x-
sin2x
=2（
cos2x-
sin2x）
=2cos（2x+
），
令2kπ≤2x+
≤2kπ+π，
解得kπ-
≤x≤kπ+
，k∈Z，
∴函数f（x）的单调递减区间为[kπ-
，kπ+
]，k∈Z；
（2）由（1）可得f（θ）=2cos（2θ+
）=-
，
解得cos（2θ+
）=-
，
∵θ∈（
，
），∴2θ+
∈（π，
），
∴sin（2θ+
）=-
=-
，
∴cos2θ=cos[（2θ+
）-
]=
cos（2θ+
）+
sin（2θ+
）
=
×(-
)+
×(-
)=-
| 3 |
=2（
| 1 |
| 2 |
| ||
| 2 |
=2cos（2x+
| π |
| 3 |
令2kπ≤2x+
| π |
| 3 |
解得kπ-
| π |
| 6 |
| 2π |
| 3 |
∴函数f（x）的单调递减区间为[kπ-
| π |
| 6 |
| 2π |
| 3 |
（2）由（1）可得f（θ）=2cos（2θ+
| π |
| 3 |
| 4 |
| 3 |
解得cos（2θ+
| π |
| 3 |
| 2 |
| 3 |
∵θ∈（
| π |
| 3 |
| 7π |
| 12 |
| π |
| 3 |
| 3π |
| 2 |
∴sin（2θ+
| π |
| 3 |
1-cos2(2θ+
|
| ||
| 3 |
∴cos2θ=cos[（2θ+
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
=
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
2+
| ||
| 6 |
点评：本题考查三角函数公式，涉及三角函数的单调性以及同角三角函数的基本关系，属中档题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
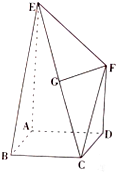如图，四边形ABCD是边长为2的正方形，AE⊥面ABCD，DF∥AE，AE=4，G为EC的中点，且GF∥面ABCD．
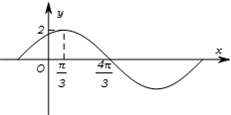已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜
已知