题目内容
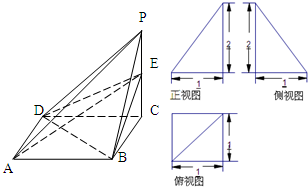 已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.(1)求证:BD⊥AE;
(2)若E为PC的中点,求直线BE与平面PBD所成角的正弦值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(1)要证BD⊥AE,只要证BD⊥面PAC,只需证BD⊥AC,BD⊥PC;
(2)要求直线BE与平面PBD所成角的正弦值,必须找到直线BE在平面PBD内的射影,由(1)易找面PBD的垂线,归结为解直角三角形.
(2)要求直线BE与平面PBD所成角的正弦值,必须找到直线BE在平面PBD内的射影,由(1)易找面PBD的垂线,归结为解直角三角形.
解答:
(1)证明:由已知PC⊥BC,PC⊥DC,BC∩DC=C,
∴PC⊥面ABCD
∵BD?面ABCD,
∴BD⊥PC,
∵BD⊥AC,PC∩AC=C,
∴BD⊥面PAC,
又∵AE?面PAC,∴BD⊥AE.
(2)解;连AC交BD于点O,连PO,
由(1)知BD⊥面PAC,∴面BED⊥面PAC,
过点E作EH⊥PO于H,则EH⊥面PBD,
∴∠EBH为BE与平面PBD所成的角.
∵EH=
,BE=
,
∴sin∠EBH=
=
.
∴PC⊥面ABCD
∵BD?面ABCD,
∴BD⊥PC,
∵BD⊥AC,PC∩AC=C,
∴BD⊥面PAC,
又∵AE?面PAC,∴BD⊥AE.
(2)解;连AC交BD于点O,连PO,
由(1)知BD⊥面PAC,∴面BED⊥面PAC,
过点E作EH⊥PO于H,则EH⊥面PBD,
∴∠EBH为BE与平面PBD所成的角.
∵EH=
| 1 |
| 3 |
| 2 |
∴sin∠EBH=
| ||
|
| ||
| 6 |
点评:本题考查简单的空间图形的三视图,和线面垂直的判定和性质定理,以及线面角的求法等知识,综合性强,思维跨度大,体现了转化的思想方法,属中档题.

练习册系列答案
相关题目
 已知
已知