题目内容
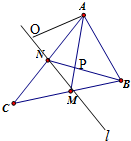在△ABC中，已知AB=2，AC=6，∠BAC=60°，中线AM、BN交于点P，设| AB |
| c |
| AC |
| b |
（1）用
| b |
| c |
| AM |
| BN |
| CP |
| CP |
（2）若直线l是BC的中垂线，O是l上一动点，求
| AO |
| BC |
考点：平面向量数量积的运算,向量的模
专题：平面向量及应用
分析：（1）利用向量的平行四边形法则、三角形的重心定理、数量积的性质即可得出；
（2）利用中垂线的性质可得
•
=0．再利用向量的三角形法则和数量积的性质可得
•
=(
+
)•
=
•
=-
(
+
)•(
-
)，即可得出．
（2）利用中垂线的性质可得
| OM |
| BC |
| AO |
| BC |
| OM |
| MA |
| BC |
| MA |
| BC |
| 1 |
| 2 |
| AC |
| AB |
| AC |
| AB |
解答：
解：（1）设CP交AB于点D．
∵中线AM、BN交于点P，设
=
，
=
，
∴
=
(
+
)=
(
+
)，
=
(
+
)=
(
+
-
)=
(-2
+
)=-
+
，
=
=
×
(
+
)=
(-
+
-
)=-
+
．
∵AB=2，AC=6，∠BAC=60°，
∴
2=(-
+
)2=
2+
2-
•
=
×62+
×22-
×6×2×cos60°
=
．
（2）∵OM⊥BC，∴
•
=0．
∵
=
+
，
=
-
．
∴
•
=(
+
)•
=
•
=-
(
+
)•(
-
)
=-
(
2-
2)
=-
(62-22)
=-16．
∵中线AM、BN交于点P，设
| AB |
| c |
| AC |
| b |
∴
| AM |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| c |
| b |
| BN |
| 1 |
| 2 |
| BA |
| BC |
| 1 |
| 2 |
| BA |
| AC |
| AB |
| 1 |
| 2 |
| AB |
| AC |
| c |
| 1 |
| 2 |
| b |
| CP |
| 2 |
| 3 |
| CD |
| 2 |
| 3 |
| 1 |
| 2 |
| CA |
| CB |
| 1 |
| 3 |
| AC |
| AB |
| AC |
| 2 |
| 3 |
| b |
| 1 |
| 3 |
| c |
∵AB=2，AC=6，∠BAC=60°，
∴
| CP |
| 2 |
| 3 |
| b |
| 1 |
| 3 |
| c |
| 4 |
| 9 |
| b |
| 1 |
| 9 |
| c |
| 4 |
| 9 |
| b |
| c |
=
| 4 |
| 9 |
| 1 |
| 9 |
| 4 |
| 9 |
=
| 124 |
| 9 |
（2）∵OM⊥BC，∴
| OM |
| BC |
∵
| AO |
| OM |
| MA |
| BC |
| AC |
| AB |
∴
| AO |
| BC |
| OM |
| MA |
| BC |
=
| MA |
| BC |
=-
| 1 |
| 2 |
| AC |
| AB |
| AC |
| AB |
=-
| 1 |
| 2 |
| AC |
| AB |
=-
| 1 |
| 2 |
=-16．
点评：本题考查了向量的平行四边形法则、三角形的重心定理、数量积的性质、中垂线的性质、向量的三角形法则等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
若0＜b＜a＜1，则在ab，ba，aa，bb中最大值是（ ）
| A、ba |
| B、aa |
| C、ab |
| D、bb |
如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，D1E⊥CD，AB=2BC=2．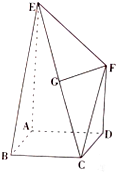
如图，四边形ABCD是边长为2的正方形，AE⊥面ABCD，DF∥AE，AE=4，G为EC的中点，且GF∥面ABCD．
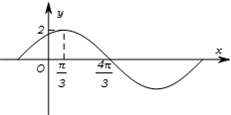已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜
已知