题目内容
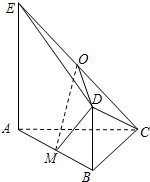 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=| 1 |
| 2 |
(1)求证:OD∥平面ABC;
(2)求直线CD和平面ODM所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:对第(1)问,取AC中点F,连结FO,FB,先证四边形BDOF为平行四边形,即得OD∥FB,再由线面平行的判定定理得证;
对第(2)问,以C为坐标原点,直线CA为x轴,直线CB为y轴,过C且垂直于平面ABC的直线为z轴建立空间直角坐标系,求得平面ODM的一个法向量
,通过向量
与
的夹角探求直线CD和平面ODM所成角的正弦值.
对第(2)问,以C为坐标原点,直线CA为x轴,直线CB为y轴,过C且垂直于平面ABC的直线为z轴建立空间直角坐标系,求得平面ODM的一个法向量
| n |
| n |
| CD |
解答:
解:(1)证明:如右图所示,取AC中点F,连结FO,FB,则FO为△CAE的中位线,∴FO∥AE,且FO=
AE,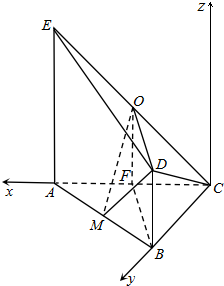
∵BD∥AE,BD=
AE,∴FO∥BD,且FO=BD,∴四边形BDOF为平行四边形,∴OD∥FB,
又∵OD?平面ABC,FB?平面ABC,∴OD∥平面ABC.
(2)如右图所示,以C为坐标原点,直线CA为x轴,直线CB为y轴,过C且垂直于平面ABC的直线为z轴建立空间直角坐标系,
由题中数据知,C(0,0,0),D(0,4,2),M(2,2,0),O(2,0,2),
则
=(0,4,2),
=(-2,4,0),
=(0,-2,2),
设平面ODM的法向量为
=(x,y,z),则
,得
,即
,
取y=1,得平面ODM的一个法向量为(2,1,1),从而cos<
,
>=
=
=
,
设直线CD和平面ODM所成的角为θ,则θ+<
,
>=90°,故sinθ=cos<
,
>=
,
即直线CD和平面ODM所成角的正弦值为
.
| 1 |
| 2 |

∵BD∥AE,BD=
| 1 |
| 2 |
又∵OD?平面ABC,FB?平面ABC,∴OD∥平面ABC.
(2)如右图所示,以C为坐标原点,直线CA为x轴,直线CB为y轴,过C且垂直于平面ABC的直线为z轴建立空间直角坐标系,
由题中数据知,C(0,0,0),D(0,4,2),M(2,2,0),O(2,0,2),
则
| CD |
| OD |
| MO |
设平面ODM的法向量为
| n |
|
|
|
取y=1,得平面ODM的一个法向量为(2,1,1),从而cos<
| n |
| CD |
| ||||
|
|
| 4×1+2×1 | ||||
|
| ||
| 10 |
设直线CD和平面ODM所成的角为θ,则θ+<
| n |
| CD |
| n |
| CD |
| ||
| 10 |
即直线CD和平面ODM所成角的正弦值为
| ||
| 10 |
点评:1.本题考查了线面平行的判定,关键是在已知平面内找一条线与已知直线平行,将线面平行转化为线线平行,将空间线面平行问题转化为平面线线平行问题,是解决空间几何问题的一种常用的化归思想.证线线平行的方法有:
①同位角相等,或内错角相等,或同旁内角互补.
②公理4:平行于同一直线的两直线互相平行.
③构造或寻找中位线(三角形、平行四边形、梯形的中位线)、利用平行直线截线段成比例.常用手段是获取分点或中点,中点可借助平行四边形对角线的交点、等腰三角形底边中点等,必要时应添加辅助线.
④平行四边形的性质(对边互相平行).
2.还考查了线面角的求法,关键是寻找已知平面的一个法向量,将线面角转化为两向量夹角问题来处理,特别注意两向量夹角与线面角之间的关系:若两向量夹角为钝角,则线面角为此钝角减去90°;若两向量的夹角为锐角,则线面角为90°减去此锐角.
①同位角相等,或内错角相等,或同旁内角互补.
②公理4:平行于同一直线的两直线互相平行.
③构造或寻找中位线(三角形、平行四边形、梯形的中位线)、利用平行直线截线段成比例.常用手段是获取分点或中点,中点可借助平行四边形对角线的交点、等腰三角形底边中点等,必要时应添加辅助线.
④平行四边形的性质(对边互相平行).
2.还考查了线面角的求法,关键是寻找已知平面的一个法向量,将线面角转化为两向量夹角问题来处理,特别注意两向量夹角与线面角之间的关系:若两向量夹角为钝角,则线面角为此钝角减去90°;若两向量的夹角为锐角,则线面角为90°减去此锐角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)=ax3+bx-4其中a,b为常数,若f(-2)=7,则f(2)的值等于( )
| A、15 | B、-7 | C、14 | D、-15 |
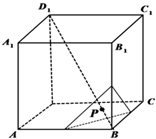 如图,正方体ABCD-A1B1C1D1的棱长为
如图,正方体ABCD-A1B1C1D1的棱长为| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
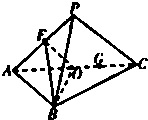 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,O分别为PA,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,O分别为PA,AC的中点,AC=16,PA=PC=10.