题目内容
已知直线l1:ax+2y+1=0,直线l2:x-y+a=0.
(1)若直线l1⊥l2,求a的值及垂足P的坐标;
(2)若直线l1∥l2,求a的值及直线l1与l2的距离.
(1)若直线l1⊥l2,求a的值及垂足P的坐标;
(2)若直线l1∥l2,求a的值及直线l1与l2的距离.
考点:直线的一般式方程与直线的平行关系,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:(1)由垂直可得a×1+2×(-1)=0,解得a值可得直线的方程,联立方程可解交点坐标;
(2)当直线l1∥l2时,
=
≠
,解得a值可得直线的方程,由平行线间的距离公式可得答案.
(2)当直线l1∥l2时,
| a |
| 1 |
| 2 |
| -1 |
| 1 |
| a |
解答:
解:(1)∵直线l1:ax+2y+1=0,直线l2:x-y+a=0,
当直线l1⊥l2时,a×1+2×(-1)=0,
解得a=2,
∴l1:2x+2y+1=0,直线l2:x-y+2=0,
联立解得
∴a的值为2,垂足P的坐标为(-
,
);
(2)当直线l1∥l2时,
=
≠
,
解得a=-2,
∴l1:-2x+2y+1=0,直线l2:-2x+2y+4=0,
由平行线间的距离公式可得d=
=
∴a的值为-2,直线l1与l2的距离为
当直线l1⊥l2时,a×1+2×(-1)=0,
解得a=2,
∴l1:2x+2y+1=0,直线l2:x-y+2=0,
联立解得
|
∴a的值为2,垂足P的坐标为(-
| 5 |
| 4 |
| 3 |
| 4 |
(2)当直线l1∥l2时,
| a |
| 1 |
| 2 |
| -1 |
| 1 |
| a |
解得a=-2,
∴l1:-2x+2y+1=0,直线l2:-2x+2y+4=0,
由平行线间的距离公式可得d=
| |1-4| | ||
|
3
| ||
| 4 |
∴a的值为-2,直线l1与l2的距离为
3
| ||
| 4 |
点评:本题考查直线的一般式方程及平行垂直关系,涉及平行线间的距离公式,属基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
已知函数f(x)=
若f(x)=2,则x的值为( )
|
| A、log32 |
| B、log23 |
| C、32 |
| D、2 |
在R上定义运算?:x?y=x(l-y).若对任意x>2,不等式(x-a)?x≤a+2都成立,则实数a的取值范围是( )
| A、[一1,7] |
| B、(一∞,3] |
| C、(一∞,7] |
| D、(一∞,-1]U[7,+∞) |
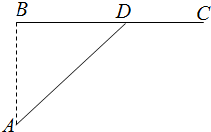 如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ