题目内容

已知
a
={3λ，6，λ+6}，
b
={λ+1，3，2λ}，若
a
∥
b
，则λ=
 
．
考点：平面向量的坐标运算
专题：平面向量及应用
分析：利用向量共线定理即可得出．
解答： 解：∵
a
={3λ，6，λ+6}，
b
={λ+1，3，2λ}，
a
∥
b
，
∴
a
=m
b

∴
3λ=m(λ+1)
6=3m
λ+6=2mλ

解得
λ=2
故答案为：2
点评：本题考查了向量共线定理，属于基础题．
练习册系列答案
相关题目
若f（x）=
2x+3，x＞0
0，x=0
ax+b，x＜0
，是奇函数，则a+b的值是
 
．
集合{2，-1}={2，a2-2a}，则实数a=
 
．
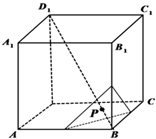如图，正方体ABCD-A1B1C1D1的棱长为
3
，动点P在对角线BD1上，过点P作垂直于BD1的平面α，记这样得到的截面多边形（含三角形）的周长为y，设BP=x，则当x∈[
1
2
，
5
2
]时，函数y=f（x）的值域为（　　）
A、[
6
，3
6
]
B、[
3
6
2
，3
6
]
C、[
3
6
2
，9]
D、[
6
，9]
在△ABC中，给出下列5个命题：
（1）若A＜B，则sinA＜sinB；        （2）sinA＜sinB若，则A＜B；
（3）若A＞B，则cot2A＞cot2B；      （4）若A＞B，则cos2A＜cos2B；
（5）若A＜B，则tan
A
2
＜tan
B
2
；
其中正确命题的序号是
 
．
若f（x）是R上的奇函数，且在R上是增函数．若对于任意x∈R都有f(cos2x+2msinx-
5
2
)＜0恒成立．求实数m的取值范围．
已知圆心为C的圆，满足下列条件：圆心C位于x轴正半轴上，与直线3x-4y+7=0相切，且被y轴截得的弦长为2
3
，圆C的面积小于13．
（1）求圆C的标准方程；
（2）若圆C上有两点M、N关于直线x+2y-1=0对称，且|MN|=2
3
，求直线MN的方程；
（3）设过点P（0，3）的直线l与圆C交于不同的两点A，B，以OA，OB为邻边作平行四边形OADB．是否存在这样的直线l，使得直线OD与PC恰好平行？如果存在，求出l的方程；如果不存在，请说明理由．
从正方体ABCD-A1B1C1D1的6个表面中选取3个面，其中有2个面不相邻的选法共有（　　）
A、8种B、12种
C、16种D、20种
已知函数f（x）=
3x(x≤1)
-x(x＞1)
若f（x）=2，则x的值为（　　）
A、log32
B、log23
C、32
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网