题目内容
复数z=
的虚部是（ ）
| -3+i |
| 2+i |
| A、1 | B、-i | C、i | D、-1 |
考点：复数代数形式的乘除运算,复数的基本概念
专题：数系的扩充和复数
分析：利用复数的运算法则和虚部的意义即可得出．
解答：
解：复数z=
=
=
=-1+i．
∴复数z的虚部是1．
故选：A．
| -3+i |
| 2+i |
| (-3+i)(2-i) |
| (2+i)(2-i) |
| -5+5i |
| 5 |
∴复数z的虚部是1．
故选：A．
点评：本题考查了复数的运算法则和虚部的意义，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
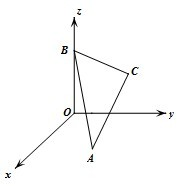如图，空间直角坐标系Oxyz中，正三角形ABC的顶点A，B分别在xOy平面和z轴上移动．若AB=2，则点C到原点O的最远距离为（ ）A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
直线l：y=k（x-2）+2与圆C：x2+y2-2x-2y=0有两个不同的公共点，则k的取值范围是（ ）
| A、（一∞，一1） |
| B、（一1，1） |
| C、（一1，+∞） |
| D、（一∞，一1）∪（一1，+∞） |
已知函数f（x）=x-[x]，x∈R，其中[x]表示不超过x的最大整数，如[-
]=-2，[-3]=-3，[
]=2，则f（x）的值域是（ ）
| 3 |
| 2 |
| 5 |
| 2 |
| A、（0，1） |
| B、（0，1] |
| C、[0，1） |
| D、[0，1] |
若f（x）=xex，则f′（1）=（ ）
| A、0 | B、e |
| C、2e | D、e2 |
已知集合M={x||x|＜3}，集合N={x|（x+4）（x-2）≤0}，则M∩N=（ ）
| A、{x|-4＜x≤3} |
| B、{x|-3＜x≤2} |
| C、{x|-3＜x＜2} |
| D、{x|-4≤x≤2} |
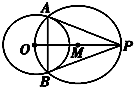如图，已知P为⊙O外一点，以PO为直径作⊙M，⊙M交⊙O于A、B两点，求证：PA、PB是⊙O的切线．