题目内容
在正项等比数列{an}中,公比q∈(0,1),a3+a5=5且a3和a5的等比中项是2.
(1)求数列{an}的通项公式;
(2)若bn=
(log2a1+log2a2+…+log2an),判断数列{bn}的前n项和Sn是否存在最大值,若存在,求出使Sn最大时n的值;若不存在,请说明理由.
(1)求数列{an}的通项公式;
(2)若bn=
| 1 |
| n |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(1)由题意可得a3•a5=4,a3+a5=5,可解得 a3=4,a5=1.进而可求q,a1,由等比数列的通项公式可得an;
(2)由(1)可得log2an=5-n,进而可得bn,易判断数列{bn}的项的符号变化规律,由各项符号可得结论;
(2)由(1)可得log2an=5-n,进而可得bn,易判断数列{bn}的项的符号变化规律,由各项符号可得结论;
解答:
解:(1)依题意:a3•a5=4,
又a3+a5=5,且公比q∈(0,1),
解得 a3=4,a5=1.
∴q2=
=
, 即q=
,
∴a1=
=16,
∴an=a1•qn-1=16•(
)n-1=25-n.
(2)∵log2an=5-n,
∴bn=
(4+3+…+(5-n))=
=
,
∵当n<9时,bn>0,当n=9时,bn=0,当n>9时,bn<0,
∴S1<S2<…<S8=S9>S10>S11>….
∴Sn有最大值,此时n=8或n=9.
又a3+a5=5,且公比q∈(0,1),
解得 a3=4,a5=1.
∴q2=
| a5 |
| a3 |
| 1 |
| 4 |
| 1 |
| 2 |
∴a1=
| a3 |
| q2 |
∴an=a1•qn-1=16•(
| 1 |
| 2 |
(2)∵log2an=5-n,
∴bn=
| 1 |
| n |
| ||
| n |
| 9-n |
| 2 |
∵当n<9时,bn>0,当n=9时,bn=0,当n>9时,bn<0,
∴S1<S2<…<S8=S9>S10>S11>….
∴Sn有最大值,此时n=8或n=9.
点评:本题考等差数列的通项公式、等比中项及数列求和,考查方程思想,考查学生解决问题的能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知x∈R,i为虚数单位,若(1-i)(x+i)=1+i,则x的值等于( )
| A、0 | B、-1 | C、1 | D、2 |
复数z=
的虚部是( )
| -3+i |
| 2+i |
| A、1 | B、-i | C、i | D、-1 |
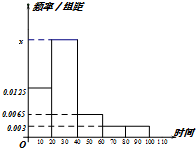 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].