如图.空间直角坐标系Oxyz中.正三角形ABC的顶点A.B分别在xOy平面和z轴上移动．若AB=2.则点C到原点O的最远距离为( ) A.3-1B.2C.3+1D.3 题目和参考答案——青夏教育精英家教网—

题目内容

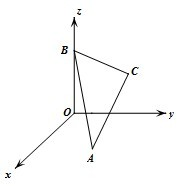如图，空间直角坐标系Oxyz中，正三角形ABC的顶点A，B分别在xOy平面和z轴上移动．若AB=2，则点C到原点O的最远距离为（　　）

A、

-1

B、2

C、

D、3

考点：点、线、面间的距离计算

专题：计算题,空间位置关系与距离

分析：连结OA，取AB的中点E，连结OE、CE，根据题意算出OE=

AB=1、CE=

AB=

，因此OC的最大值等于OE、CE两条线段的和，由此即可得到本题的答案．

解答： 解：连结OA，取AB的中点E，连结OE、CE，根据题意可得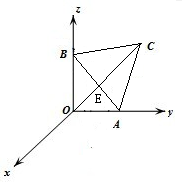

∵Rt△AOB中，斜边AB=2，∴OE=

AB=1，
又∵正△ABC的边长为2，
∴CE=

AB=

，
对图形加以观察，当A，B分别在xOy平面和z轴上移动时，
可得当O、E、C三点共线时，C到原点O的距离最远，且这最远距离等于

+1
故答案为：C

点评：本题给出空间坐标系内的动点，求点到原点O的最远距离．着重考查了线面垂直的性质、直角三角形与等边三角形的特征等知识，属于中档题．

练习册系列答案

相关题目

在△ABC中，a、b、c分别为角A、B、C的对边，若

若圆（x+a）²+（y+b）²=r²（r＞0）的圆心在第二象限，则直线y=ax+b必不经过（　　）

A、第一象限	B、第二象限
C、第三象限	D、第四象限

函数f（x）=mx³+（m+1）x²+x+2，若f′（1）=18，则m=（　　）

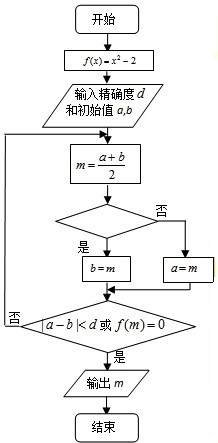如图是用二分法求方程f（x）=0近似解的程序框图，其中f（a）f（b）＜0．判断框内可以填写的内容有如下四个选择：
①f（a）f（m）＜0；
②f（a）f（m）＞0；
③f（b）f（m）＜0；
④f（b）f（m）＞0．
其中正确的是（　　）

点（2，3）到3x+4y+2=0的距离是（　　）

定义区间（a，b），[a，b），（a，b]，[a，b]的长度均为d=b-a，多个区间并集的长度为各区间长度之和，例如，（-2，-1）∪[3，5）的长度d=[（-1）-（-2）]+（5-3）=3．用[x]表示不超过x的最大整数，记{x}=x-[x]，其中x∈R．设f（x）=[x]•{x}，g（x）=x-1，当0≤x≤5时，则不等式f（x）＜g（x）的解集区间的长度为（　　）

已知x∈R，i为虚数单位，若（1-i）（x+i）=1+i，则x的值等于（　　）

试题分类