题目内容
直线l：y=k（x-2）+2与圆C：x2+y2-2x-2y=0有两个不同的公共点，则k的取值范围是（ ）
| A、（一∞，一1） |
| B、（一1，1） |
| C、（一1，+∞） |
| D、（一∞，一1）∪（一1，+∞） |
考点：直线与圆相交的性质
专题：直线与圆
分析：由已知条件，求出圆心、半径、圆心到直线的距离，再由直线与圆有两个交点知：圆心到直线的距离小于半径，由此能求出k的取值范围．
解答：
解：圆C：x2+y2-2x-2y=0中，
圆心C（1，1），
圆半径r=
=
，
圆心C（1，1）到直线l：y=k（x-2）+2的距离：
d=
=
，
∵直线l：y=k（x-2）+2与圆C：x2+y2-2x-2y=0有两个不同的公共点，
∴d＜r，即
＜
，
整理，得（k+1）2＞0，
解得k≠-1．
∴k的取值范围是（-∞，-1）∪（-1，+∞）．
故选：D．
圆心C（1，1），
圆半径r=
| 1 |
| 2 |
| 4+4 |
| 2 |
圆心C（1，1）到直线l：y=k（x-2）+2的距离：
d=
| |k-1-2k+2| | ||
|
| |1-k| | ||
|
∵直线l：y=k（x-2）+2与圆C：x2+y2-2x-2y=0有两个不同的公共点，
∴d＜r，即
| |1-k| | ||
|
| 2 |
整理，得（k+1）2＞0，
解得k≠-1．
∴k的取值范围是（-∞，-1）∪（-1，+∞）．
故选：D．
点评：本题考查直线 的参数的取值范围的求法，是中档题，解题时要注意点到直线的距离公式的应用．
练习册系列答案
相关题目
若圆（x+a）2+（y+b）2=r2（r＞0）的圆心在第二象限，则直线y=ax+b必不经过（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知x∈R，i为虚数单位，若（1-i）（x+i）=1+i，则x的值等于（ ）
| A、0 | B、-1 | C、1 | D、2 |
已知函数g（x）是偶函数，f（x）=g（x-2），且当x≠2时其导函数f（x）满足（x-2）f′（x）＞0，若1＜a＜3，则（ ）
| A、f（4a）＜f（3）＜f（log3a） |
| B、f（3）＜f（log3a）＜f（4a） |
| C、f（log3a）＜f（3）＜f（4a） |
| D、f（log3a）＜f（4a）＜f（3） |
设P=e0.2，Q=ln0.2，R=sin
，则（ ）
| 15π |
| 7 |
| A、P＜R＜Q |
| B、R＜Q＜P |
| C、R＜P＜Q |
| D、Q＜R＜P |
已知a，b∈R．下列四个条件中，使a＞b成立的必要条件是（ ）
| A、a＞b-1 |
| B、a＞b+1 |
| C、丨a丨＞丨b丨 |
| D、a-1＞b-1 |
复数z=
的虚部是（ ）
| -3+i |
| 2+i |
| A、1 | B、-i | C、i | D、-1 |
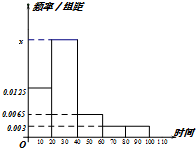某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．