题目内容
若f（x）=xex，则f′（1）=（ ）
| A、0 | B、e |
| C、2e | D、e2 |
考点：导数的运算
专题：计算题,导数的概念及应用
分析：直接根据基本函数的导数公式和导数的运算法则求解即可．
解答：
解：∵f（x）=xex，
∴f′（x）=ex+xex，
∴f′（1）=2e．
故选：C．
∴f′（x）=ex+xex，
∴f′（1）=2e．
故选：C．
点评：本题考查了基本函数的导数公式和导数的运算法，属于送分题．
练习册系列答案
相关题目
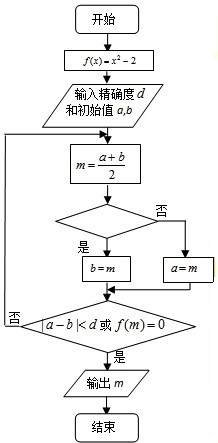如图是用二分法求方程f（x）=0近似解的程序框图，其中f（a）f（b）＜0．判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0；
②f（a）f（m）＞0；
③f（b）f（m）＜0；
④f（b）f（m）＞0．
其中正确的是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
已知函数g（x）是偶函数，f（x）=g（x-2），且当x≠2时其导函数f（x）满足（x-2）f′（x）＞0，若1＜a＜3，则（ ）
| A、f（4a）＜f（3）＜f（log3a） |
| B、f（3）＜f（log3a）＜f（4a） |
| C、f（log3a）＜f（3）＜f（4a） |
| D、f（log3a）＜f（4a）＜f（3） |
已知a，b∈R．下列四个条件中，使a＞b成立的必要条件是（ ）
| A、a＞b-1 |
| B、a＞b+1 |
| C、丨a丨＞丨b丨 |
| D、a-1＞b-1 |
命题p：“?x∈Z，x2≥0”，则?p为（ ）
| A、?x∈Z，x2＜0 |
| B、?x∉Z，x2＜0 |
| C、?x0∈Z，x02≥0 |
| D、?x0∈Z，x02＜0 |
复数z=
的虚部是（ ）
| -3+i |
| 2+i |
| A、1 | B、-i | C、i | D、-1 |