题目内容
直线l经过点P(1,9),且与两坐标轴的正半轴相交,当两截距之和最小时直线l的方程为 .
考点:直线的截距式方程
专题:直线与圆
分析:设所求直线l方程为
+
=1(a,b>0).由于直线l经过点P(1,9),可得
+
=1.再利用“乘1法”和基本不等式的性质即可得出.
| x |
| a |
| y |
| b |
| 1 |
| a |
| 9 |
| b |
解答:
解:设所求直线l方程为
+
=1(a,b>0).
∵直线l经过点P(1,9),
∴
+
=1.
∴a+b=(a+b)(
+
)=10+
+
≥10+2
=16,当且仅当b=3a=12时取等号.
∴直线l的方程为
+
=1,化为3x+y-12=0.
故答案为:3x+y-12=0.
| x |
| a |
| y |
| b |
∵直线l经过点P(1,9),
∴
| 1 |
| a |
| 9 |
| b |
∴a+b=(a+b)(
| 1 |
| a |
| 9 |
| b |
| b |
| a |
| 9a |
| b |
|
∴直线l的方程为
| x |
| 4 |
| y |
| 12 |
故答案为:3x+y-12=0.
点评:本题考查了“乘1法”和基本不等式的性质、直线的截距式,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
在△ABC中,
=(cos23°,sin23°),
=(2sin22°,2cos22°),则△ABC的面积为( )
| AB |
| AC |
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=-sin
x在区间[0,t]上至少取得2个最大值,则正整数t的最小值是( )
| π |
| 3 |
| A、9 | B、10 | C、11 | D、12 |
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )


| A、72cm3 |
| B、60cm3 |
| C、48cm3 |
| D、36cm3 |
某程序框图如图所示,则该程序运行后输出的a的值为( )


| A、1 | B、0 | C、-1 | D、2 |
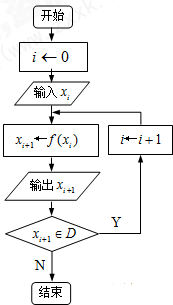 对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.