题目内容
11．函数y=cos（2x-1）的导数为（ ）| A． | y'=-2sin（2x-1） | B． | y'=-2cos（2x-1） | C． | y'=-sin（2x-1） | D． | y'=-cos（2x-1） |
分析 根据复合函数的求导公式求导即可
解答 解：函数y=cos（2x-1）的导数为y′=-sin（2x-1）•（2x-1）′=-2sin（2x-1），
故选：A
点评 本题考查了复合函数的求导公式，属于基础题
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
1．若函数f（x）=x2由x=1至x=1+△x的平均变化率的取值范围是（1.975，2.025），则增量△x的取值范围为（ ）
| A． | （-0.025，0.025） | B． | （0，0.025） | C． | （0.025，1） | D． | （-0.025，0） |
19．两个相关变量满足如下关系：
则两变量的回归方程为（ ）
| x | 10 | 15 | 20 | 25 | 30 |
| y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A． | $\widehat{y}$=0.56x+997.4 | B． | $\widehat{y}$=0.63x-231.2 | C． | $\widehat{y}$=0.56x+501.4 | D． | $\widehat{y}$=60.4x+400.7 |
20．
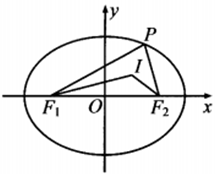设P为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的动点，F1、F2为椭圆C的焦点，I为△PF1F2的内心，则直线IF1和直线IF2的斜率之积（ ）
设P为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的动点，F1、F2为椭圆C的焦点，I为△PF1F2的内心，则直线IF1和直线IF2的斜率之积（ ）| A． | 是定值 | B． | 非定值，但存在最大值 | ||
| C． | 非定值，但存在最小值 | D． | 非定值，且不存在最值 |