Question

已知O为坐标原点，点M的坐标为（1，-1），点N（x，y）的坐标x，y满足

x+2y-3≤0 x+3y-3≥0 y≤1

，则

OM

•

ON

＜0的概率为

 

．

Answer 1

考点：简单线性规划,几何概型

专题：概率与统计

分析：先根据约束条件画出可行域得到其面积，再利用向量的数量积表示出z=

OM

•

ON

，得到z＜0时的区域，进而得到

OM

•

ON

＜0的区域面积，即可求得概率．

解答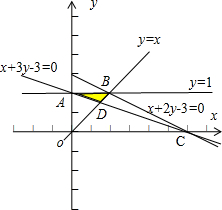： 解：N（x，y）的坐标x，y满足不等式组

x+2y-3≤0 x+3y-3≥0 y≤1

，
表示的可行域如图：
由于A（0，1），B（1，1），C（3，0），则可行域的面积为：S_△ABC=

1

2

×1×1=

1

2

由向量的数量积的几何意义可知，z=

OM

•

ON

=（1，-1）•（x，y）=x-y，
则

OM

•

ON

＜0即x-y＜0，如图中阴影部分所示，
由于D（

3

4

，

3

4

），则阴影部分的面积为S_△ABD=

1

2

×1×(1-

3

4

)=

1

8

则

OM

•

ON

＜0的概率P为

1 8

1 2

=

1

4

．
故答案为：

1

4

．

点评：本题主要考查了简单线性规划的应用、向量的数量积以及几何概型等知识，属于中档题．