题目内容
如图，F是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
（Ⅰ）求椭圆的方程：
（Ⅱ）过点A的直线l2与圆M交于PQ两点，且
| MP |
| MQ |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）由已知条件求出B（0，
c），C（3c，0），F（-c，0），由此求出圆M的方程为（x-c）2+y2=4c2，再由圆M与直线l1：x+
y+3=0相切，解得c=1，a=2，b=
，由此能求出椭圆方程．
（Ⅱ）设直线l2的方程为y=k（x+2），由已知条件求出∠PMQ=120°，从而求出k=±
，由此能求出直线l2的方程．
| 3 |
| 3 |
| 3 |
（Ⅱ）设直线l2的方程为y=k（x+2），由已知条件求出∠PMQ=120°，从而求出k=±
| ||
| 4 |
解答：
解：（Ⅰ）∵F是椭圆
+
=1（a＞b＞0）的一个焦点，A，B是椭圆的两个顶点，
椭圆的离心率为
，
∴
=
，∴
=1-
=
，∴b=
a，c=
a，
设F（-c，0），B（0，
a）=（0，
c），
∵kBF=
=
，BC⊥BF，
∴kBC=-
，∴
=
，∴xC=
b=
a•
=
a=3c，
∴C（3c，0），
设圆M的方程为x2+y2+Dx+Ey+F=0，
把B（0，
c），C（3c，0），F（-c，0）代入，得：
，
解得D=-2c，E=0，F=-3c2，
∴圆M的方程为（x-c）2+y2=4c2，
∵圆M与直线l1：x+
y+3=0相切，
∴
=2c，解得c=1，
∴a=2，b=
，
∴所求的椭圆方程为
+
=1．
（Ⅱ）∵A是椭圆方程为
+
=1的左顶点，∴A（-2，0），
∵圆M的方程为（x-1）2+y2=4，
∴过点A斜率不存在的直线与圆不相交，
∴设直线l2的方程为y=k（x+2），
∵
•
=-2，又|
|=|
|=2，
∴cos＜
，
＞=
=-
，
∴∠PMQ=120°，
圆心M到直线l2的距离d=
r=1，
∴
=1，解得k=±
，
∴直线l2的方程为y=±
（x+2）．
| x2 |
| a2 |
| y2 |
| b2 |
椭圆的离心率为
| 1 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
| c2 |
| a2 |
| b2 |
| a2 |
| 1 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
设F（-c，0），B（0，
| ||
| 2 |
| 3 |
∵kBF=
| b |
| c |
| 3 |
∴kBC=-
| ||
| 3 |
| b |
| xC |
| ||
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∴C（3c，0），
设圆M的方程为x2+y2+Dx+Ey+F=0，
把B（0，
| 3 |
|
解得D=-2c，E=0，F=-3c2，
∴圆M的方程为（x-c）2+y2=4c2，
∵圆M与直线l1：x+
| 3 |
∴
|1×c+
| ||
|
∴a=2，b=
| 3 |
∴所求的椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
（Ⅱ）∵A是椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
∵圆M的方程为（x-1）2+y2=4，
∴过点A斜率不存在的直线与圆不相交，
∴设直线l2的方程为y=k（x+2），
∵
| MP |
| MQ |
| MP |
| MQ |
∴cos＜
| MP |
| MQ |
| ||||
|
|
| 1 |
| 2 |
∴∠PMQ=120°，
圆心M到直线l2的距离d=
| 1 |
| 2 |
∴
| |k+2k| | ||
|
| ||
| 4 |
∴直线l2的方程为y=±
| ||
| 4 |
点评：本题考查椭圆方程的求法，考查直线方程的求法，综合性强，难度大，解题时要注意等价转化思想的合理运用．
练习册系列答案
相关题目
在区间[-2，3]上任取一个数a，则函数f（x）=x2-2ax+a+2有零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
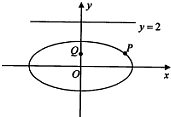已知椭圆C：
如图，F1（-c，0），F2（c，0）分别是双曲线C：