题目内容
已知函数f(x)=
(其中p为常数,x∈[-2,2]),若对任意的x,都有f(x)=f(-x)
(1)求p的值;
(2)用定义证明函数f(x)在(0,2)上是单调减函数;
(3)若p=1,求函数f(x)的值域.
| px+2 |
| x2+1 |
(1)求p的值;
(2)用定义证明函数f(x)在(0,2)上是单调减函数;
(3)若p=1,求函数f(x)的值域.
考点:函数单调性的判断与证明,函数单调性的性质,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)因为f(x)是偶函数,所以f(-x)=f(x)任意x∈R恒成立,代入解析式结合比较系数法,可得实数p的值;
(2)由(1)知函数解析式为f(x)=
,再设0<x1<x2<2,f(x1)与f(x2)作差,因式分解后经过讨论可得f(x1)>f(x2),因此,函数f(x)在(0,2)上是单调减函数;
(3)利用导数,结合函数图象进行求解.
(2)由(1)知函数解析式为f(x)=
| 2 |
| x2+1 |
(3)利用导数,结合函数图象进行求解.
解答:
解:(1)∵f(x)是偶函数,
∴
=
,
可得2px=0对任意x∈R恒成立,故p=0.
(2)由(1)知函数解析式为f(x)=
,
设0<x1<x2<2,
∵f(x1)-f(x2)=
-
=
,
∵x1<x2,
∴x2-x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(0,2)上是单调减函数;
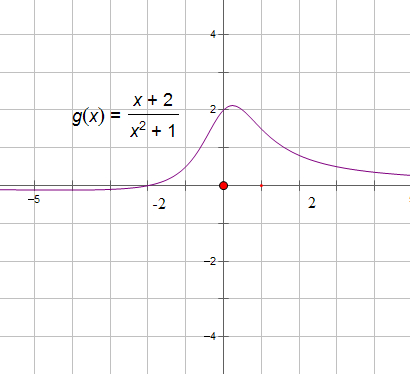
(3)∵p=1,
∴y=
,其图象如下图所示:
根据图象,得到f′(x)=
,
f′(x)=0,∴x=-2±
,
当x=-2+
时,函数有最大值,
f(-2+
)=
=
,
=
-1,
∴y∈[0,
-1].
∴
| -px+2 |
| x2+1 |
| px+2 |
| x2+1 |
可得2px=0对任意x∈R恒成立,故p=0.
(2)由(1)知函数解析式为f(x)=
| 2 |
| x2+1 |
设0<x1<x2<2,
∵f(x1)-f(x2)=
| 2 |
| x12+1 |
| 2 |
| x22+1 |
=
| 2(x2-x1)(x2+x1) |
| (x12+1)(x22+1) |
∵x1<x2,
∴x2-x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(0,2)上是单调减函数;
(3)∵p=1,
∴y=
| x+2 |
| x2+1 |

根据图象,得到f′(x)=
| x2+1-2x(x+2) |
| (x2+1)2 |
f′(x)=0,∴x=-2±
| 5 |
当x=-2+
| 5 |
f(-2+
| 5 |
-2+
| ||
(-2+
|
| ||
10-4
|
=
| ||
| 2 |
∴y∈[0,
| ||
| 2 |
点评:本题在含有参数的分式函数的奇偶性已知的情况下,求参数的值并且讨论了函数的单调性,着重考查了函数的单调性与奇偶性等知识点,属于中档题.

练习册系列答案
相关题目
若函数f(x)=
(a∈R)是奇函数,则a的值为( )
| x+a |
| x2+1 |
| A、1 | B、0 | C、-1 | D、±1 |
某程序框图如图所示,若程序运行后,输出S的结果是( )


| A、246 | B、286 |
| C、329 | D、375 |