题目内容
已知函数f(x)=
x3+x2+ax.
(1)若f(x)在区间[1,+∞)单调递增,求a的最小值;
(2)若g(x)=
,对?x1∈[
,2],?x2∈[
,2],使f′(x1)≤g(x2)成立,求a的范围.
| 1 |
| 3 |
(1)若f(x)在区间[1,+∞)单调递增,求a的最小值;
(2)若g(x)=
| 1 |
| ex |
| 1 |
| 2 |
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)题目可转化成f′(x)=x2+2x+a≥0在[1,+∞)恒成立,再通过分离常数的方法求解;
(2)将“?x1∈[
,2],?x2∈[
,2],使f′(x1)≤g(x2)成立”转化成“[f′(x)]max≤[g(x)]max”,x∈[
,2],再进一步利用函数单调性分别求最大值.
(2)将“?x1∈[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)依题意知,f′(x)=x2+2x+a≥0在[1,+∞)恒成立,
∴a≥-x2-2x=-(x+1)2+1,而y=-(x+1)2+1在[1,+∞)单调递减,从而ymax=-3,
∴只需a≥-3.
∴amin=-3.
(2)对?x1∈[
,2],?x2∈[
,2],使f′(x1)≤g(x2),
即[f′(x)]max≤[g(x)]max,f′(x)=(x+1)2+a-1在[
,2]单调递增,
∴f′(x)max=f′(2)=8+a,
g(x)在[
,2]上单调递减,则g(x)max=g(
)=
,
∴8+a≤
,则a≤
-8.
∴a≥-x2-2x=-(x+1)2+1,而y=-(x+1)2+1在[1,+∞)单调递减,从而ymax=-3,
∴只需a≥-3.
∴amin=-3.
(2)对?x1∈[
| 1 |
| 2 |
| 1 |
| 2 |
即[f′(x)]max≤[g(x)]max,f′(x)=(x+1)2+a-1在[
| 1 |
| 2 |
∴f′(x)max=f′(2)=8+a,
g(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| e |
∴8+a≤
| ||
| e |
| ||
| e |
点评:本题都需要将原题意转化成我们更为熟悉的知识,从而进一步给出解答.第一问中,学生往往容易忽视f′(x)≥0中的等号,从而造成错误;在第二问中,
对于“?”“?”的理解至关重要,需要我们更多的理解,才能够准确的转化题意,进行进一步解答.
对于“?”“?”的理解至关重要,需要我们更多的理解,才能够准确的转化题意,进行进一步解答.

练习册系列答案
相关题目
按如图程序框图来计算,若输入x=10,则运算的次数为( )

| A、6 | B、5 | C、4 | D、3 |
设数列{an},{an2} (n∈N*)都是等差数列,若a1=2,则a22+a33+a44+a55等于( )
| A、60 | B、62 | C、63 | D、66 |
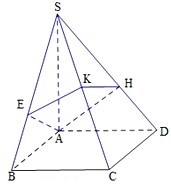 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.