题目内容
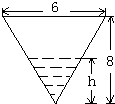 将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度.
将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度.考点:函数模型的选择与应用,导数的运算,利用导数研究函数的单调性
专题:函数的性质及应用,导数的概念及应用
分析:由题,依据图形得出V关于高度h的函数及高度h关于t的函数,利用导数研究其变化规律即可得出水面上升的速度.
解答:
解:设注入水tmin后,水深为hm,由相似三角形对应边成比例可
得水面直径为
hm,
这时水的体积为 V=
π(
h)2•h=
h3…(4分)
由于水面高度h随时间t而变化,因而h是t的函数h=h(t)
由此可得水的体积关于时间t的导数为V′t=V′h•h′t=(
h3)′•h′t=
h2•h′t
由假设,注水速度为4m3/min,4t=
h3∴4=
h2•ht′
所以当h=5时,ht'=
m/min,
当水深为5m时,水面上升的速度
m/min. …(10分)
法(2)设t时刻水面的高度为hm
则
π(
h)2h=4th(t)=
…(4分)h′(t)=
…(6分)
由h(t)=
=5t=
π…(8分)∴h′(
π)=
m/min…(10分)
得水面直径为
| 3 |
| 4 |
这时水的体积为 V=
| 1 |
| 3 |
| 3 |
| 8 |
| 3π |
| 64 |
由于水面高度h随时间t而变化,因而h是t的函数h=h(t)
由此可得水的体积关于时间t的导数为V′t=V′h•h′t=(
| 3π |
| 64 |
| 9π |
| 64 |
由假设,注水速度为4m3/min,4t=
| 3π |
| 64 |
| 9π |
| 64 |
所以当h=5时,ht'=
| 256 |
| 225π |
当水深为5m时,水面上升的速度
| 256 |
| 225π |
法(2)设t时刻水面的高度为hm
则
| 1 |
| 3 |
| 3 |
| 8 |
| 3 |
| ||
| 3 |
| ||
| 1 | ||
3t
|
由h(t)=
| 3 |
| ||
| 375 |
| 256 |
| 375 |
| 256 |
| 256 |
| 225π |
点评:本题考查建立函数模型及利用导数研究实际问题中事物变化的规律,导数在实际问题中有着广泛的运用

练习册系列答案
相关题目
已知x,y之间的数据如下表所示,则y与x之间的线性回归方程必过点( )
| x | 1.08 | 1.12 | 1.19 | 1.30 |
| y | 2.25 | 2.37 | 2.40 | 2.60 |
| A、(0,0) |
| B、(1.17,0) |
| C、(0,2.41) |
| D、(1.17,2.41) |
 读该程序图(其中x满足:0<x<12)
读该程序图(其中x满足:0<x<12)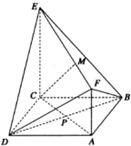 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2