题目内容
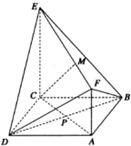 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2| 2 |
| ME |
| FM |
(1)求证:CM∥平面BDF;
(2)求平面ADF与平面BDF的夹角的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)可知CD、CB、CE两两垂直.建立如图空间直角坐标系C-xyz.利用
∥
证出CM∥OF;
(2)先求出平面ADF与平面BDF的一个法向量,利用两法向量的夹角求出二面角A-DF-B的大小.
| CM |
| OF |
(2)先求出平面ADF与平面BDF的一个法向量,利用两法向量的夹角求出二面角A-DF-B的大小.
解答:
 (1)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,
(1)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,
所以CE⊥面ABCD.
所以CD、CB、CE两两垂直.
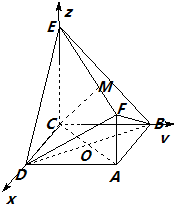
可建立如图空间直角坐标系C-xyz.
则(2,0,0),A(2,2,0),B(0,2,0),F(2,2,
),E(0,0,2
,O(1,1,0)
由
=2
,可求得M(
,
,
)
所以
=(
,
,
),
=(1,1,
).
所以
=
所以
∥
,
所以CM∥OF;
(2)解:因为CD⊥平面ADF,所以平面ADF的法向量
=(2,0,0).
设平面BDF的法向量为
=(x,y,1),则
.
所以法向量
=(-
,
,1),
所以<
,
>=
=-
所以<
,
>=
,
由图可知二面角A-DF-B为锐角,
所以求平面ADF与平面BDF的夹角的大小为
.
 (1)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,
(1)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,所以CE⊥面ABCD.
所以CD、CB、CE两两垂直.
可建立如图空间直角坐标系C-xyz.
则(2,0,0),A(2,2,0),B(0,2,0),F(2,2,
| 2 |
| 2 |
由
| ME |
| FM |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
所以
| CM |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| OF |
| 2 |
所以
| CM |
| 4 |
| 3 |
| OF |
所以
| CM |
| OF |
所以CM∥OF;
(2)解:因为CD⊥平面ADF,所以平面ADF的法向量
| CD |
设平面BDF的法向量为
| n |
|
所以法向量
| n |
| ||
| 2 |
| ||
| 2 |
所以<
| CD |
| n |
-
| ||
2×
|
| 1 |
| 2 |
所以<
| CD |
| n |
| 2π |
| 3 |
由图可知二面角A-DF-B为锐角,
所以求平面ADF与平面BDF的夹角的大小为
| π |
| 3 |
点评:本题考查直线和平面平行的判定,异面直线夹角,二面角的计算,利用了空间向量的方法.要注意相关点和向量坐标的准确性,及转化时角的相等或互余关系.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
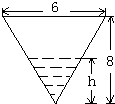 将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度.
将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度.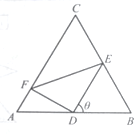 如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).
如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°). 如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AD=3,BC=2,AB=
如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AD=3,BC=2,AB=