题目内容
已知复数ω=(m2-2m-3)+(m2-m-12)i,(m∈R,i为虚单位).
(1)若ω为实数,求m的值;
(2)若复数ω对应的点在第四象限,求实数m的取值范围.
(1)若ω为实数,求m的值;
(2)若复数ω对应的点在第四象限,求实数m的取值范围.
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:(1)若ω为实数,则其实部为0,解方程m2-m-12=0即可求得m的值;
(2)复数ω对应的点在第四象限,则
,解此不等式组即可求得实数m的取值范围.
(2)复数ω对应的点在第四象限,则
|
解答:
解:(1)因为ω=(m2-2m-3)+(m2-m-12)i为实数,
所以m2-m-12=0,
解得:m=-3或m=4…(6分);
(2)由复数ω对应点第四象限得:
,即
,…(10分)
所以-3<m<-1或3<m<4 …(14分)
所以m2-m-12=0,
解得:m=-3或m=4…(6分);
(2)由复数ω对应点第四象限得:
|
|
所以-3<m<-1或3<m<4 …(14分)
点评:本题考查复数的代数表示法及其几何意义,着重考查解方程与解不等式组的运算能力,属于中档题.

练习册系列答案
相关题目
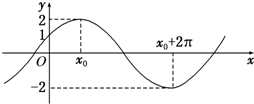 如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<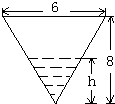 将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度.
将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度. 如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AD=3,BC=2,AB=
如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AD=3,BC=2,AB=