题目内容
求函数y=sin2（2x+
）的导数．
| π |
| 3 |
考点：简单复合函数的导数,导数的运算
专题：导数的概念及应用
分析：法一：利用复合函数的求导公式直接求导；
法二：先用二倍角公式降幂，再利用复合函数的导数公式求导．
法二：先用二倍角公式降幂，再利用复合函数的导数公式求导．
解答：
解：法一：y′=2sin(2x+
)•[sin(2x+
)]′=2sin(2x+
)cos(2x+
)•(2x+
)′=2sin(4x+
)…（10分）
法二：∵y=sin2(2x+
)=
…（5分）
∴y=(
)′+
×sin(4x+
)×(4x+
)′=2sin(4x+
)…（10分）
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
法二：∵y=sin2(2x+
| π |
| 3 |
1-cos(4x+
| ||
| 2 |
∴y=(
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
点评：本题考查复合函数的导数及二倍角公式，属于基本计算题，对相应的运算规则要熟练掌握
练习册系列答案
相关题目
已知平面向量
，
满足|
|=1，|
|=2，且（
-
）⊥
，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
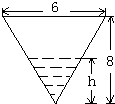将水注入锥形容器中，其速度为4m3/min，设锥形容器的高为8m，顶口直径为6m，求当水深为5m时，水面上升的速度．