题目内容
求函数y=2x+2+9•2-x的最小值.
考点:基本不等式在最值问题中的应用,指数型复合函数的性质及应用
专题:函数的性质及应用,不等式的解法及应用
分析:可将函数解答式变为y=4×2x+9•2-x再用基本不等式求最值
解答:
解:y=2x+2+9•2-x=4×2x+9•2-x≥2
=12,
等号当且仅当4×2x=9•2-x时,即x=log436等号成立
故函数y=2x+2+9•2-x的最小值为12.
| 4×2x×9×2-x |
等号当且仅当4×2x=9•2-x时,即x=log436等号成立
故函数y=2x+2+9•2-x的最小值为12.
点评:本题考查基本不等式在最值中的应用,积为定值或和为定值是可用基本不等式求最值的特征

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知sinxcosy=
,则cosxsiny的取值范围是( )
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
| D、[-1,1] |
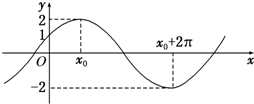 如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<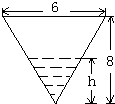 将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度.
将水注入锥形容器中,其速度为4m3/min,设锥形容器的高为8m,顶口直径为6m,求当水深为5m时,水面上升的速度. 如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AD=3,BC=2,AB=
如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AD=3,BC=2,AB=