题目内容
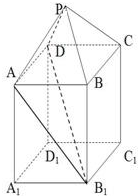 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=| 2 |
(1)证明:PD⊥平面PBC;
(2)若A1A=2,证明:PC∥平面AB1D;
(3)若A1A=a,试求当a为何值时,PC∥平面AB1D?
考点:直线与平面平行的判定,直线与平面平行的性质,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证明PD⊥平面PBC,只需证明PD垂直于平面PBC的两条相交直线即可,由 PD=PC=
可得PD⊥PC,而ABCD-A1B1C1D1是一个长方体,容易证明BC⊥面CC1D1D,而P∈平面CC1D1D,所以PD?面CC1D1D,容易得到PD⊥BC,从而得证;
(2)证明PC∥C1D,利用线面平行的判定定理,可得结论.
(3)当a=2时,PC∥平面AB1D,利用线面平行的判定可得结论.
| 2 |
(2)证明PC∥C1D,利用线面平行的判定定理,可得结论.
(3)当a=2时,PC∥平面AB1D,利用线面平行的判定可得结论.
解答:
(1)证明:因为 PD=PC=
,CD=AB=2,
所以△PCD为等腰直角三角形,所以PD⊥PC.
因为ABCD-A1B1C1D1是一个长方体,
所以BC⊥面CC1D1D,而P∈平面CC1D1D,
所以PD?面CC1D1D,所以BC⊥PD.
因为PD垂直于平面PBC内的两条相交直线PC和BC,
由线面垂直的判定定理,可得PD⊥平面PBC.
(2)解:长方体中AD∥BC,AD=BC,BC∥B1C1,BC=B1C1,
所以AD∥B1C1,AD=B1C1
即A,D,B1,C1共面,
长方体中DD1=AA1=a=2,CD=AB=2,四边形CC1D1D是一个正方形,∠C1DC=45°,
而∠PCD=45°,且CD、C1D与PC在同一个平面内,
所以PC∥C1D.
又C1D?面AB1C1D,PC?面AB1C1D,
所以PC∥面AB1C1D,即PC∥平面AB1D.
(3)解:当a=2时,PC∥平面AB1D.
当a=2时,四边形CC1D1D是一个正方形,所以∠C1DC=45°,
而∠PDC=45°,所以∠PDC1=90°,所以C1D⊥PD.
而PC⊥PD,C1D与PC在同一个平面内,所以PC∥C1D.
而C1D?面AB1C1D,所以PC∥面AB1C1D,所以PC∥平面AB1D.
| 2 |
所以△PCD为等腰直角三角形,所以PD⊥PC.
因为ABCD-A1B1C1D1是一个长方体,
所以BC⊥面CC1D1D,而P∈平面CC1D1D,
所以PD?面CC1D1D,所以BC⊥PD.
因为PD垂直于平面PBC内的两条相交直线PC和BC,
由线面垂直的判定定理,可得PD⊥平面PBC.
(2)解:长方体中AD∥BC,AD=BC,BC∥B1C1,BC=B1C1,
所以AD∥B1C1,AD=B1C1
即A,D,B1,C1共面,
长方体中DD1=AA1=a=2,CD=AB=2,四边形CC1D1D是一个正方形,∠C1DC=45°,
而∠PCD=45°,且CD、C1D与PC在同一个平面内,
所以PC∥C1D.
又C1D?面AB1C1D,PC?面AB1C1D,
所以PC∥面AB1C1D,即PC∥平面AB1D.
(3)解:当a=2时,PC∥平面AB1D.
当a=2时,四边形CC1D1D是一个正方形,所以∠C1DC=45°,
而∠PDC=45°,所以∠PDC1=90°,所以C1D⊥PD.
而PC⊥PD,C1D与PC在同一个平面内,所以PC∥C1D.
而C1D?面AB1C1D,所以PC∥面AB1C1D,所以PC∥平面AB1D.
点评:本题考查线面垂直,考查线面平行,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列函数是偶函数,且在(0,+∞)上是增函数的是( )
A、f(x)=(
| ||
B、f(x)=x
| ||
| C、f(x)=lnx | ||
| D、f(x)=-x2+4 |