题目内容
已知x∈[0,1],函数f(x)=x2-ln(x+
),g(x)=x3-3a2x-4a.
(1)求函数f(x)的单调区间和值域;
(2)设a≤-1,若?x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
| 1 |
| 2 |
(1)求函数f(x)的单调区间和值域;
(2)设a≤-1,若?x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导数f′(x)=2x-
=
;从而由导数的正负确定函数的单调区间及值域;
(2)设g(x)在[0,1]上的值域为[b,c],则有b≤
且c≥ln2;再求导g′(x)=3x2-3a2,从而确定函数的单调性,从而化为最值问题.
| 1 | ||
x+
|
| (x+1)(2x-1) | ||
x+
|
(2)设g(x)在[0,1]上的值域为[b,c],则有b≤
| 1 |
| 4 |
解答:
解:(1)f′(x)=2x-
=
;
令f′(x)<0解得,0≤x<
;
故函数f(x)的单调减区间为[0,
],
此时,
≤f(x)≤ln2;
令f′(x)>0解得,
<x≤1;
故函数f(x)的单调增区间[
,1],
此时,
≤f(x)≤ln3-ln2;
故函数f(x)的值域为[
,ln2].
(2)根据所给条件,设g(x)在[0,1]上的值域为[b,c],
则有b≤
且c≥ln2;
g′(x)=3x2-3a2<0,
g(x)在[0,1]上是单调减函数,
故g(0)=-4a≥ln2,
解得a≤-
;
g(1)=1-3a2-4a≤
,
解得a≤-
或a≥
;
故a≤-
.
| 1 | ||
x+
|
| (x+1)(2x-1) | ||
x+
|
令f′(x)<0解得,0≤x<
| 1 |
| 2 |
故函数f(x)的单调减区间为[0,
| 1 |
| 2 |
此时,
| 1 |
| 4 |
令f′(x)>0解得,
| 1 |
| 2 |
故函数f(x)的单调增区间[
| 1 |
| 2 |
此时,
| 1 |
| 4 |
故函数f(x)的值域为[
| 1 |
| 4 |
(2)根据所给条件,设g(x)在[0,1]上的值域为[b,c],
则有b≤
| 1 |
| 4 |
g′(x)=3x2-3a2<0,
g(x)在[0,1]上是单调减函数,
故g(0)=-4a≥ln2,
解得a≤-
| ln2 |
| 4 |
g(1)=1-3a2-4a≤
| 1 |
| 4 |
解得a≤-
| 3 |
| 2 |
| 1 |
| 6 |
故a≤-
| 3 |
| 2 |
点评:本题考查了导数的综合应用及函数的性质应用,同时考查了恒成立问题,属于中档题.

练习册系列答案
相关题目
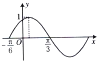 函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
与圆x2+(y+5)2=9相切,且在两坐标轴上截距相等的直线共有( )条.
| A、2 | B、3 | C、4 | D、6 |
投球3次,事件A1表示“投中i次”,其中i=0,1,2,3.那么A=A1∪A2∪A3表示的是( )
| A、全部投中 | B、必然投中 |
| C、至少有1次投中 | D、投中3次 |
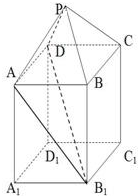 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=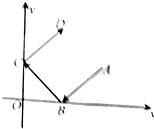 如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的
如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的