题目内容
椭圆
+
=1与双曲线
-
=1有公共的焦点F1,F2,则双曲线的渐近线方程为 .
| x2 |
| 6 |
| y2 |
| 2 |
| x2 |
| 3 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆的焦点,可得双曲线的c=2,再由双曲线的a,b,c的关系可得b=1,再由双曲线的渐近线方程即可得到.
解答:
解:椭圆
+
=1的焦点为(±2,0),
则双曲线的c=2,
即有3+b2=4,解得,b=1.
则双曲线
-y2=1的渐近线方程为y=±
x.
故答案为:y=±
x.
| x2 |
| 6 |
| y2 |
| 2 |
则双曲线的c=2,
即有3+b2=4,解得,b=1.
则双曲线
| x2 |
| 3 |
| ||
| 3 |
故答案为:y=±
| ||
| 3 |
点评:本题考查椭圆和双曲线的方程和性质,考查双曲线的渐近线方程的求法,属于基础题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
双曲线
-
=1的焦点坐标是( )
| x2 |
| 36 |
| y2 |
| 64 |
| A、(0,-10),(0,10) | ||||
| B、(-10,0),(10,0) | ||||
C、(-2
| ||||
D、(0,-2
|
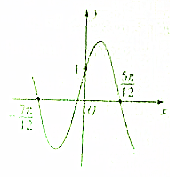 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
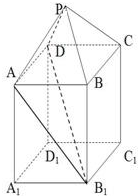 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=