题目内容
已知一元二次不等式ax2+bx+c<0的解集为B,集合A={x|x∈z},且A∩B={-1,0},则不等式可以是 .
考点:一元二次不等式的解法
专题:开放型,不等式的解法及应用
分析:根据题意,得出集合B的取值是什么,利用一元二次不等式与对应方程的关系,得出不等式是什么即可.
解答:
解:∵一元二次不等式ax2+bx+c<0的解集为B,集合A={x|x∈z},且A∩B={-1,0},
∴{-1,0}⊆B,
可设B=(m,n),
则
,
且
;
不妨令m=3,n=-2,则a=1,b=-1,c=-6;
∴不等式是x2-x-6<0.
故答案为:x2-x-6<0.
∴{-1,0}⊆B,
可设B=(m,n),
则
|
且
|
不妨令m=3,n=-2,则a=1,b=-1,c=-6;
∴不等式是x2-x-6<0.
故答案为:x2-x-6<0.
点评:本题考查了一元二次不等式的解法与应用问题,答案是不唯一的,是开放性题目.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
“a>b”是“a+1>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设数列{an}(n∈N*)是公差为d的等差数列,若a2=4,a4=6,则d=( )
| A、4 | B、3 | C、2 | D、1 |
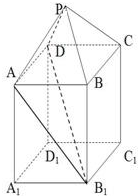 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=