题目内容
下列函数是偶函数,且在(0,+∞)上是增函数的是( )
A、f(x)=(
| ||
B、f(x)=x
| ||
| C、f(x)=lnx | ||
| D、f(x)=-x2+4 |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:根据基本初等函数的奇偶性与单调性,对选项中的函数进行判断即可.
解答:
解:对于A,f(x)=(
)x是定义域R上的非奇非偶的函数,∴不满足题意;
对于B,f(x)=x
是定义域R上的偶函数,且在(0,+∞)上是增函数,∴满足题意;
对于C,f(x)=lnx是定义域(0,+∞)上的非奇非偶的函数,∴不满足题意;
对于D,f(x)=-x2+4是定义域R上的偶函数,在(0,+∞)上是减函数,∴不满足题意.
故选:B.
| 1 |
| 2 |
对于B,f(x)=x
| 2 |
| 3 |
对于C,f(x)=lnx是定义域(0,+∞)上的非奇非偶的函数,∴不满足题意;
对于D,f(x)=-x2+4是定义域R上的偶函数,在(0,+∞)上是减函数,∴不满足题意.
故选:B.
点评:本题考查了常见的基本初等函数的奇偶性与单调性的应用问题,是基础题目.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
投球3次,事件A1表示“投中i次”,其中i=0,1,2,3.那么A=A1∪A2∪A3表示的是( )
| A、全部投中 | B、必然投中 |
| C、至少有1次投中 | D、投中3次 |
已知变量x,y满足约束条件
,则目标函数z=y-3x的取值范围是( )
|
A、[-6,
| ||
B、[1,
| ||
| C、[-6,1] | ||
D、[-
|
“a>b”是“a+1>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
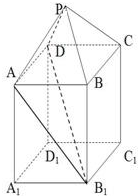 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,AB=2,BC=3,点P∈平面CC1D1D,且PD=PC=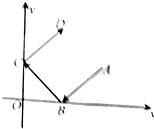 如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的
如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的