题目内容
已知△ABC三内角A，B，C所对的边分别为a，b，c，重心为G（三角形中三边中线的交点），若2a
+3b
=3c
，则cosB= ．
| GA |
| GB |
| CG |
考点：余弦定理,平面向量的基本定理及其意义
专题：解三角形,平面向量及应用
分析：根据重心的性质及向量加法的平行四边形法则得到
=-
(
-2
)，
=-
(-2
+
)，
=
(
+
)分别带入2a
+3b
=3c
并根据平面向量基本定理可得到
，这两式相减便得
．所以根据余弦定理即可求出cosB．
| GA |
| 1 |
| 3 |
| CB |
| CA |
| GB |
| 1 |
| 3 |
| CB |
| CA |
| CG |
| 1 |
| 3 |
| CB |
| CA |
| GA |
| GB |
| CG |
|
|
解答：
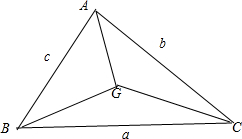解：如图，
根据重心的性质及向量加法的平行四边形法则：
=-
(
+
)=-
(
-
+
)=-
(
-2
)；
=-
(
+
)=-
(-2
+
)；
=
(
+
)；
∴-
(
-2
)-b(-2
+
)=c(
+
)；
即：(2b-
)
+(
-b)
=c
+c
；
∴
；
∴
；
由余弦定理cosB=
=
=
．
故答案为：
．
解：如图，根据重心的性质及向量加法的平行四边形法则：
| GA |
| 1 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| CB |
| CA |
| AC |
| 1 |
| 3 |
| CB |
| CA |
| GB |
| 1 |
| 3 |
| BA |
| BC |
| 1 |
| 3 |
| CB |
| CA |
| CG |
| 1 |
| 3 |
| CB |
| CA |
∴-
| 2a |
| 3 |
| CB |
| CA |
| CB |
| CA |
| CB |
| CA |
即：(2b-
| 2a |
| 3 |
| CB |
| 4a |
| 3 |
| CA |
| CB |
| CA |
∴
|
∴
|
由余弦定理cosB=
| a2+c2-b2 |
| 2ac |
| a2 | ||
|
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：考查重心的性质：重心到顶点距离是它到对边中点距离的2倍，向量加法的平行四边形法则，以及平面向量基本定理，余弦定理．
练习册系列答案
相关题目
设函数f1（x）=x，f2（x）=log2014x，f3（x）=
，ai=
i=1，2，…，2015，记Ik=|fk（a2）-fk（a1）|+|fk（a3）-fk（a2）|+…+|fk（a2015）-fk（a2014）|，k=1，2，3 则（ ）
| 1 |
| x |
| i |
| 2015 |
| A、I1＜I3＜I2 |
| B、I1＜I2＜I3 |
| C、I2＜I1＜I3 |
| D、I3＜I2＜I1 |
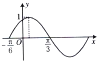函数f（x）=sin（ωx+φ）（x∈R）（ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知球的直径SC=6，A，B，是该球球面上的两点，AB=3，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为（ ）
A、
| ||||
B、4
| ||||
C、
| ||||
D、6
|
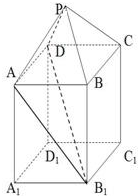如图，在组合体中，ABCD-A1B1C1D1是一个长方体，P-ABCD是一个四棱锥，AB=2，BC=3，点P∈平面CC1D1D，且PD=PC=