题目内容
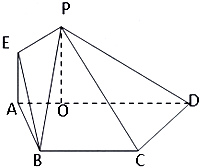 如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=
如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=| 1 |
| 2 |
| 3 |
| 2 |
(1)证明:BE∥平面PCD.
(2)求该几何体的体积.
考点:组合几何体的面积、体积问题
专题:计算题,证明题
分析:(1)在平面PCD内作直线FC,利用直线与平面平行的判定定理证明BE∥平面PCD.
(2)分割几何体为两个棱锥,利用已知数据即可求该几何体的体积.
(2)分割几何体为两个棱锥,利用已知数据即可求该几何体的体积.
解答:
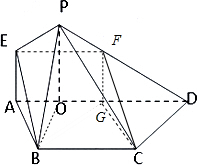 解:(1)作EF∥AD,交PD于F,连结FC,OB,作FG∥EA,交AD于G,连结GC,
解:(1)作EF∥AD,交PD于F,连结FC,OB,作FG∥EA,交AD于G,连结GC,
∵AD∥BC,AB=BC=CD=
AD=2,EF∥AD,
∴AEFG是矩形,∵BC
AG,∴EF
BC,
∴BCFE是平行四边形,BE∥CF,CF?面PCD,BE?面PCD,
∴BE∥平面PCD.
(2)由题意,几何体看作P-BCDO,B-POAE两个棱锥的体积的和,
∵EA⊥平面ABCD,PO∥EA,∴PO⊥平面ABCD,
∵AO=1,平面外两点P,E满足PO=
,AE=1,等腰梯形ABCD中,AD∥BC,AB=BC=CD=
AD=2,
∴BO⊥平面PEAO,
∴几何体的体积为:VP-BCDO+VB-POAE=
×
×
×
+
×
×1×
=
.
 解:(1)作EF∥AD,交PD于F,连结FC,OB,作FG∥EA,交AD于G,连结GC,
解:(1)作EF∥AD,交PD于F,连结FC,OB,作FG∥EA,交AD于G,连结GC,∵AD∥BC,AB=BC=CD=
| 1 |
| 2 |
∴AEFG是矩形,∵BC
| ∥ |
. |
| ∥ |
. |
∴BCFE是平行四边形,BE∥CF,CF?面PCD,BE?面PCD,
∴BE∥平面PCD.
(2)由题意,几何体看作P-BCDO,B-POAE两个棱锥的体积的和,
∵EA⊥平面ABCD,PO∥EA,∴PO⊥平面ABCD,
∵AO=1,平面外两点P,E满足PO=
| 3 |
| 2 |
| 1 |
| 2 |
∴BO⊥平面PEAO,
∴几何体的体积为:VP-BCDO+VB-POAE=
| 1 |
| 3 |
| 2+3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
1+
| ||
| 2 |
| 3 |
5
| ||
| 3 |
点评:本题考查直线与平面平行的证明,判定定理的应用,几何体的体积的求法,考查逻辑推理能力与计算能力.

练习册系列答案
相关题目
已知正数a,b满足:三数a,1,b的倒数成等差数列,则a+b的最小值为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
已知x0是函数f(x)=(
)x-
的一个零点,若x1∈(0,x0),x2∈(x0,+∞),则( )
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
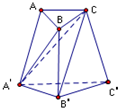 如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )
如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )| A、1:1:1 |
| B、2:1:1 |
| C、4:2:1 |
| D、4:4:1 |
 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=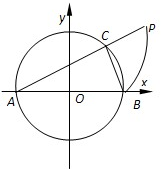 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )