题目内容
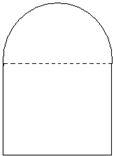要在墙上开一个上半部为半圆形、下部为矩形的窗户（如图所示），在窗框为定长的条件下，要使窗户能够透过最多的光线，窗户应设计成怎样的尺寸？考点：基本不等式在最值问题中的应用
专题：应用题,函数的性质及应用
分析：根据窗户面积为：一个矩形的面积+半圆的面积，分别表示出利用二次函数最值求法得出边长即可．
解答：
解：∵窗框的用料是am，
∴假设AD=2x，AB=
，
∴窗子的面积为：S=2x•
+
πx2=（-
-4）x2+ax，
当x=
时，此时面积最大，窗户能够透过最多的光线．
∴AD=
，AB=
，
∴半圆直径与矩形的高的比为2：1，窗户能够透过最多的光线．
解：∵窗框的用料是am，∴假设AD=2x，AB=
| a-πx-4x |
| 2 |
∴窗子的面积为：S=2x•
| a-πx-4x |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
当x=
| a |
| 8+π |
∴AD=
| 2a |
| 8+π |
| 2a |
| 8+π |
∴半圆直径与矩形的高的比为2：1，窗户能够透过最多的光线．
点评：本题主要考查了函数模型的选择与应用，以及圆的面积和二次函数的性质，同时考查了计算能力，属于中档题．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
已知椭圆
+
=1（a＞b＞0），F1，F2分别是椭圆的左、右焦点，椭圆上总存在点P使得PF1⊥PF2，则椭圆的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||||
B、（
| ||||
C、（0，
| ||||
D、（0，
|
抛物线y2=4x上一点A的横坐标为4，则点A与抛物线焦点的距离为（ ）
| A、2 | B、3 | C、4 | D、5 |
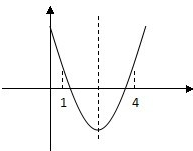已知关于x不等式x2-2ax+a+2≤0（a∈R）的解集为M．