题目内容
7个身高均不相同的学生排成一排合影留念,最高个子站在中间,从中间到左边和从中间到右边一个比一个矮,则这样的排法共有 种.
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:最高个子站在中间,只需排好左右两边,第一步:先排左边,有
=20种排法,第二步:排右边,有
=1种,根据分步乘法计数原理可得结论.
| C | 3 6 |
| C | 3 3 |
解答:
解:最高个子站在中间,只需排好左右两边,
第一步:先排左边,有
=20种排法,第二步:排右边,有
=1种,
根据分步乘法计数原理,共有20×1=20种,
故答案为:20.
第一步:先排左边,有
| C | 3 6 |
| C | 3 3 |
根据分步乘法计数原理,共有20×1=20种,
故答案为:20.
点评:本题考查计数原理的应用,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知锐角三角形的边长分别为2,4,x,则x的取值范围是( )
A、1<x<
| ||||
B、
| ||||
C、1<x<2
| ||||
D、2
|
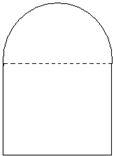 要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?