题目内容
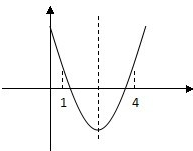 已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.
已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.(1)当M为空集时,求实数a的取值范围;
(2)如果M⊆[1,4],求实数a的取值范围.
考点:一元二次不等式与二次函数
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由于M为空集,可得△<0,解出即可;
(2)f(x)=x2-2ax+a+2=(x-a)2-a2+a+2.分类讨论:当M为空集,由(1)可得:a∈(-1,2).当M不为空集时,由于M⊆[1,4],可得
解得a的取值范围.再求其并集即可.
(2)f(x)=x2-2ax+a+2=(x-a)2-a2+a+2.分类讨论:当M为空集,由(1)可得:a∈(-1,2).当M不为空集时,由于M⊆[1,4],可得
|
解答:
解:(1)∵M为空集,
∴△=4a2-4(a+2)<0,即a2-a-2<0
∴实数a的取值范围为(-1,2)
(2)f(x)=x2-2ax+a+2=(x-a)2-a2+a+2,
①当M为空集,由(1)可得:a∈(-1,2)时,M⊆[1,4].
②当M不为空集时,
∵M⊆[1,4]
∴
即
,
解得1≤a≤
.
∴实数a的取值范围为[1,
].
综上得实数a的取值范(-1,
].
∴△=4a2-4(a+2)<0,即a2-a-2<0
∴实数a的取值范围为(-1,2)
(2)f(x)=x2-2ax+a+2=(x-a)2-a2+a+2,
①当M为空集,由(1)可得:a∈(-1,2)时,M⊆[1,4].
②当M不为空集时,
∵M⊆[1,4]
∴
|
即
|
解得1≤a≤
| 18 |
| 7 |
∴实数a的取值范围为[1,
| 18 |
| 7 |
综上得实数a的取值范(-1,
| 18 |
| 7 |
点评:本题考查了二次函数的图象与性质、一元二次不等式的解法、分类讨论方法、集合之间的关系,属于中档题.

练习册系列答案
相关题目
已知ABCD-A1B1C1D1为棱长为1的正方体,点P1,P2分别是线段AB,BD1上的动点且不包括端点,在P1,P2运动的过程中线段P1,P2始终平行平面A1ADD1,则几何体P1P2AB1的体积为最大值时,AP1=( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
下列事件为随机事件的是( )
| A、平时的百分制考试中,小强的考试成绩为105分 |
| B、边长为a,b的长方形面积为ab |
| C、100个零件中2个次品,98个正品,从中取出2个,2个都是次品 |
| D、抛一个硬币,落地后正面朝上或反面朝上 |
下列各组函数中,表示同一函数的是( )
A、y=
| ||||||
B、y=|x|与y=
| ||||||
C、y=x与y=
| ||||||
D、y=
|
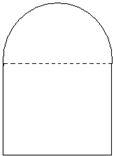 要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸? 如图,从A到B有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为ξ.
如图,从A到B有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为ξ.