题目内容
已知椭圆
+
=1(a>b>0),F1,F2分别是椭圆的左、右焦点,椭圆上总存在点P使得PF1⊥PF2,则椭圆的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||||
B、(
| ||||
C、(0,
| ||||
D、(0,
|
考点:椭圆的应用
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据椭圆上存在点P使得直线PF1与直线PF2垂直,可得|OP|=c≥b,从而可求椭圆离心率e的取值范围.
解答:
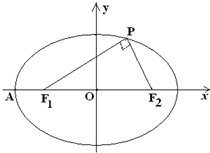 解:由PF1⊥PF2,知△F1PF2是直角三角形,
解:由PF1⊥PF2,知△F1PF2是直角三角形,
∴|OP|=c≥b,即c2≥a2-c2,
∴a≤
c,
∵e=
,0<e<1,
∴
≤e<1
故选A.
 解:由PF1⊥PF2,知△F1PF2是直角三角形,
解:由PF1⊥PF2,知△F1PF2是直角三角形,∴|OP|=c≥b,即c2≥a2-c2,
∴a≤
| 2 |
∵e=
| c |
| a |
∴
| ||
| 2 |
故选A.
点评:本题考查椭圆的几何性质,考查学生分析转化问题的能力,属于基础题.

练习册系列答案
相关题目
从圆x2-2x+y2-2y+1=0外一点P(3,2)向这个圆作两条切线,则两切线夹角的正切值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
函数y=sin(
-2x)的单调递减区间是( )
| π |
| 4 |
A、[kπ+
| ||||
B、[kπ-
| ||||
C、[2kπ-
| ||||
D、[2kπ-
|
已知ABCD-A1B1C1D1为棱长为1的正方体,点P1,P2分别是线段AB,BD1上的动点且不包括端点,在P1,P2运动的过程中线段P1,P2始终平行平面A1ADD1,则几何体P1P2AB1的体积为最大值时,AP1=( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
设集合A={x|
<2x<2},B={x|lgx>0},则A∪B=( )
| 1 |
| 2 |
| A、{x|x>-1} |
| B、{x|-1<x<1} |
| C、∅ |
| D、{x|-1<x<1或x>1} |
某台小型晚会由4个节目组成,演出顺序有如下要求:节目甲不能排在第一位,该台晚会节目演出顺序的编排方案共有( )
| A、24种 | B、18种 |
| C、12种 | D、8种 |
已知F1,F2是椭圆
+
=1(a>b>0)的两个焦点,AB是过F1的弦,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a |
| C、8a | D、2a+2b |
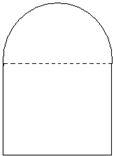 要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?