题目内容
将y=f′(x)sinx图象向左平移
个单位,得y=1-2sin2x图象,则f(x)=( )
| π |
| 4 |
| A、2cosx | B、2sinx |
| C、sinx | D、cosx |
考点:函数y=Asin(ωx+φ)的图象变换,导数的运算
专题:导数的综合应用,三角函数的图像与性质
分析:利用函数图象的平移结合y=f′(x)sinx得到f′(x+
))•sin(x+
)=f′(x+
))×
(cosx+sinx)
=1-2sin2x=cos2x=cos2x-sin2x,求出f′(x+
)后得答案.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
=1-2sin2x=cos2x=cos2x-sin2x,求出f′(x+
| π |
| 4 |
解答:
解:将函数y=f′(x)sinx的图象向左平移
个单位得到y=1-2sin2x,
又f′(x+
)•sin(x+
)=f′(x+
))×
(cosx+sinx)
=1-2sin2x=cos2x=cos2x-sin2x,
∴f′(x+
)=
(cosx-sinx)=2cos(x+
),
∴f′(x)=2cosx,
∴f(x)=2sinx.
故选:B.
| π |
| 4 |
又f′(x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
=1-2sin2x=cos2x=cos2x-sin2x,
∴f′(x+
| π |
| 4 |
| 2 |
| π |
| 4 |
∴f′(x)=2cosx,
∴f(x)=2sinx.
故选:B.
点评:本题考查了导数的运算,考查了三角函数的图象的平移,训练了函数解析式的求法,是中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
已知函数y=f(x),下列说法错误的是( )
| A、△y=f(x0+△x)-f(x0)叫函数增量 | ||||
B、
| ||||
| C、f(x)在点x0处的导数记为y′ | ||||
| D、f(x)在点x0处的导数记为f′(x0) |
下列命题中,正确的是( )
| A、底面是正方形的四棱柱是正方体 |
| B、棱锥的高线不可能在几何体之外 |
| C、过棱锥顶点的一个平面把棱锥分成两部分,每一部分形成的几何体仍然是棱锥 |
| D、在所有棱柱中,互相平行的面最多有三对 |
若|z+i|+|z-i|=4,则复平面内与复数z对应的点的轨迹是( )
| A、线段 | B、椭圆 | C、双曲线 | D、圆 |
已知a>b>c,则下列各式中正确的是( )
| A、ac2>bc2 | ||||||
| B、ab>bc | ||||||
| C、2a>2b>2c | ||||||
D、
|
已知P(3cosα,3sinα,1)和Q(2cosβ,2sinβ,1),则|PQ|的取值范围是( )
| A、[1,5] |
| B、(1,5) |
| C、[0,5] |
| D、[0,25] |
复数 z=x+yi(x,y∈R)满足方程|z-1|=2|z|,则在复平面上表示复数z的动点Z的轨迹图形是( )
| A、直线 | B、圆 | C、椭圆 | D、抛物线 |
D、E、F分别是△ABC三边BC、CA、AB中点,则
+
+
=( )
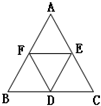
| DE |
| EF |
| DF |

A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|